1.6. Закон Дальтона для смеси газов
На практике чаще встречаются не чистые газы, а их смеси. Компоненты смеси занимают один и тот же объем и имеют одинаковую температуру. Концентрация смеси равна сумме концентраций компонентов смеси, т. е.
.
Тогда по формуле (4.5) давление смеси равно
.
Введем обозначения:
,
где
-
парциальные давления.
Парциальным давлением называется давление, которое производит на стенки сосуда данная компонента смеси. Тогда давление смеси равно
(1.15)
Формула (1.15) представляет собой закон Дальтона. Давление смеси газов равно сумме парциальных давлений.
1.7. Основные понятия классической и квантовой статистики
Классическая статистика описывает макросистемы, состоящие из микрочастиц, движение которых в рассматриваемых условиях можно описывать законами классической механики (механики Ньютона). Примером такой системы, подчиняющейся законам классической статистики является идеальный газ.
В общем случае для описания движения микрочастиц, необходимо применять законы квантовой механики. Статистическая физика, описывающая макросистемы, состоящие из микрочастиц, движение которых описывается законами квантовой механики, называется квантовой статистикой.
Одним из основных понятий статистики (как классической, так и квантовой) является вероятность. Пусть какая-либо физическая система может находиться в различных физических состояниях. Предположим, что эти состояния дискретны, т.е. характеризующие их физические величины изменяются скачками и каждое состояние характеризуется определенным значением хi некоторой физической величины х. В некоторых состояниях система будет проводить большее время, в некоторых – меньшее. Будем измерять величину х некоторое число раз N. Обозначим Ni – число измерений, каждое из которых дает значение измеряемой величины х, равное хi. Вероятность wi того, что величина х имеет значение хi, называется предел отношения числа Ni к полному числу измерений N при стремлении N к бесконечности, т.е.:
(1.16)
Дискретное значение физических величин - характерная особенность всех микрочастиц (атомов, молекул). Например, энергия вращательного и колебательного движения молекулы может меняться только дискретно, скачками. Про такую величину говорят, что она квантуется.
Вместе с тем, можно с большой точностью считать, что энергия поступательного движения молекул не квантуется, т.е. изменяется непрерывно, значит, непрерывно меняется и скорость молекул газа, а также и координата молекул в пространстве. Для непрерывной случайной величины, например, скорости молекулы v, вероятность dwv того, что скорость молекулы v принимает значения в интервале от v до v + dv вычисляется так:
(1.17)
здесь N - полное число измерений скорости, dNv - число измерений, в которых скорость молекулы попали в интервал от v до v + dv.
Очевидно, что:
(1.18)
Это следует из определения вероятности (1.17):
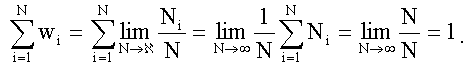
Аналогично и для непрерывной случайной величины. Из (1.18) следует, что:
(1.19)