3.4. Давление под изогнутой поверхностью жидкости

Рассмотрим поверхность жидкости, опирающуюся на некоторый плоский контур (рис. 3.5,а).

Рис. 3.5.

Если поверхность жидкости не плоская, то стремление ее к сокращению приведет к возникновению давления, дополнительного к тому, которое испытывает жидкость с плоской поверхностью. В случае выпуклой поверхно­сти это дополнительное давление положительно (рис. 3.5, 6), в случае вогнутой поверхности — отрицательно (рис. 3.5, в). В последнем случае поверхностный слой, стремясь сократиться, растягивает жидкость.

Величина добавочного давления, очевидно, должна возрастать с увеличением коэффициента поверхностного натяжения а и кривизны поверхности. Вычислим доба­вочное давление для сферической поверхности жидко­сти. Для этого рассечем мысленно сферическую каплю жидкости диаметральной плоскостью на два полушария (рис. 3.6).

Рис. 3.6. К расчету давления Лапласа.

Из-за поверхностного натяжения оба полушария притягиваются друг к другу с силой, равной

(3.14)

Эта сила прижимает друг к другу оба полушария по поверхности S = πR² и, следовательно, обусловливает дополнительное давление

(3.15)

Кривизна сферической поверхности всюду одинакова и определяется радиусом сферы R. Очевидно, что чем меньше R, тем больше кривизна сферической поверхности. Кривизну произвольной поверхности принято характеризовать так называемой средней кривизной, которая может оказаться различной для разных точек поверхности.

В случае, если поверхность имеет произвольную форму и характеризуется двумя главными радиусами и , то:

.

(3.16)

Выражение (3.16) является обобщением формулы Лапласа (3.15) на случай произвольной формы поверхности жидкости.

Если поверхность жидкости имеет цилиндрическую форму, то один из радиусов в формуле (3.16) становится бесконечным, и для этого случая формула (3.16) приобретает вид

,

(3.17)

где: - радиус цилиндрической поверхности жидкости.

4. Капиллярные явления.

Явление смачивания (или несмачивания) твердого тела жидкостью приводит к появлению капиллярного эффекта. Капилляром называется тонкая трубка, вставленная в сосуд с жидкостью. Капиллярный эффект связан с тем, что в зависимости от того, смачивает жидкость стенки капилляра или нет, внутри капилляра поверхность жидкости приобретает соответственно вогнутую или выпуклую форму(рис. 3.7).

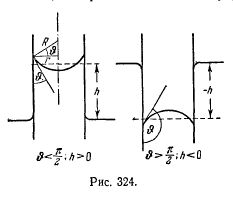
Рис. 3.7. .Капилляр в смачивающей (а) и не смачивающей (б) жидкостях

В первом случае давление внутри жидкости уменьшается по сравнению с внешним давлением, и она поднимается внутри капилляра (см. рис. 3.7 (а)). А во втором - это давление возрастает, что приводит к опусканию уровня жидкости в капилляре по отношению к её уровню в сосуде (см. рис. 3.7 (б)).

Между жидкостью в капилляре и широком сосуде устанавливается такая разность уровней h, чтобы гидро­статическое давление pgh уравновешивало капиллярное давление Δр:

(3.18)

В этой формуле а — поверхностное натяжение на границе жидкость —газ, R — радиус кривизны мениска,

Радиус кривизны мениска R можно выразить через краевой угол и радиус капилляра г. В самом деле, из рис. 3.7 видно, что R = г/cos θ. Подставив это значение в (3.18) и разрешив получившееся уравнение относительно h, приходим к формуле

(3.19)

В соответствии с тем, что смачивающая жидкость поднимается по капилляру, а несмачивающая — опускается, формула (3.19) дает в случае θ < π/2 (cosθ >0) положительные h и в случае θ >π/2 (cosθ < 0) отрицательные h.

Задача 7.1. Найти силу притяжения двух квадратных пластинок, между которыми находится слой жидкости, толщиной . Размер пластинок много больше толщины слоя жидкости. Коэффициент поверхностного натяжения жидкости равен σ. Считать, что жидкость полностью смачивает пластинки.

Решение: В соответствии с формулой Лапласа (3.15) для случая цилиндрической формы поверхности жидкости имеем выражение для разности атмосферного давления и давления внутри жидкости:

Отсюда

.

     По мере уменьшения толщины слоя жидкости, величины и растут, и это приводит к тому, что капля жидкости стремится максимально растечься между пластинами. Минимальная толщина слоя жидкости будет определяться степенью параллельности поверхностей пластинок и качеством их обработки. Чем лучше отшлифованы пластинки, тем сильнее они притягиваются. Для случая воды, находящейся между стеклянными пластинками, разность давлений может достигать величины атмосферного давления.

     Отметим, что, несмотря на достаточно большую силу притяжения пластинок, их можно легко рассоединить, сдвигая друг относительно друга вдоль плоскости поверхности.

     Задача 7.2. Найти радиус R пузырька газа, находящегося в воде при температуре T с поверхностным натяжением σ, если величина гидростатического давления воды P₀, а концентрация молекул газа равна n. Пузырек считать сферическим, а газ - идеальным.

     Решение: Согласно формуле Лапласа (3.15), давление газа в сферическом пузырьке равно

.

     В соответствии с основным уравнением молекулярно-кинетической теории

.

     Поэтому имеем

.

     Следовательно

.

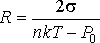     Очевидно, что давление газа в пузырьке больше гидростатического давления воды на величину давления, создаваемого поверхностным натяжением.
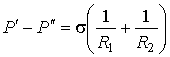