
- •Сборник задач для типового расчета
- •Тема 1: «Множества и операции над ними»
- •2 . Проверьте, справедливы ли следующие равенства:
- •3. Изобразите на координатной плоскости декартовы произведения ав, ва, аа, вв множеств а и в:
- •4. Запишите формулой графически заданные множества:
- •Тема 2-3: «Отношения и отображения»
- •5. Какими свойствами обладают следующие отношения? Являются ли они отношением эквивалентности, если да, то запишите классы эквивалентности и фактор-множество? Составить матрицу отношений и граф.
- •6. Для заданных отношений построить симметричное отношение r*, композицию r○r. Изобразить их графически. Определить, является ли данное отношение функциональным. Ответ обосновать.
- •7. Выясните, является ли заданное отношение отображением, инъективным отображением, сюръективным, биективным, обратимым? Для обратимых - найти обратную функцию.
- •8. Для заданных функций найти следующие композиции f○g, g○f, f○f, g○g.
- •Тема 4: «Алгебры»
- •9. Найдите σ1-1, σ2-2, σ23, σ14, σ2-99, σ266, σ1◦σ2, σ2◦σ1. Определите порядок, число инверсий и четность каждой из подстановок.
- •10. Найдите наибольший общий делитель чисел а и b, используя алгоритм Евклида. Составьте цепную дробь и линейную комбинацию.
- •Тема 5: «Элементы комбинаторики. Метод математической индукции»
- •11. Доказать, что для любого натурального числа n:
- •12. Какой коэффициент стоит при данном произведении в заданном разложении?
- •13. Решите задачи:
- •Тема: «Логика высказываний и предикатов. Кванторы»
- •Тема: «Графы»
- •25. В ненагруженном графе g из задачи 23 найдите:
- •27. В графе g из задачи 23 найдите:
- •29. Перечислите все неизоморфные графы с указанными свойствами и значениями параметров (в скобках указано число искомых графов):
- •3 0. Какие из данных графов являются изоморфными?
- •31. Построить плоское изображение графа, если это возможно. Если нет, то доказать, что граф не планарен.
- •32. Найти хроматическое число графа и оптимальную раскраску графа из задачи 31.

Сборник задач для типового расчета
Тема 1: «Множества и операции над ними»
1. Пусть А – множество четных натуральных чисел; В – множество нечетных натуральных чисел; С – множество натуральных чисел, не больших 10. Опишите словесно следующие множества и задайте их двумя способами.
Ā;

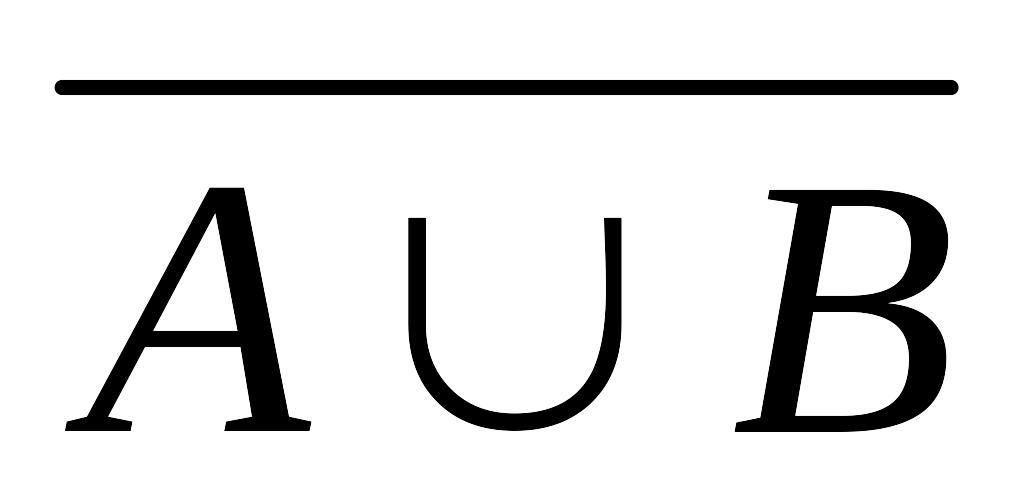

АВ
АВ



АС

ВС
АВ
АС
ВС
АВС
АВС
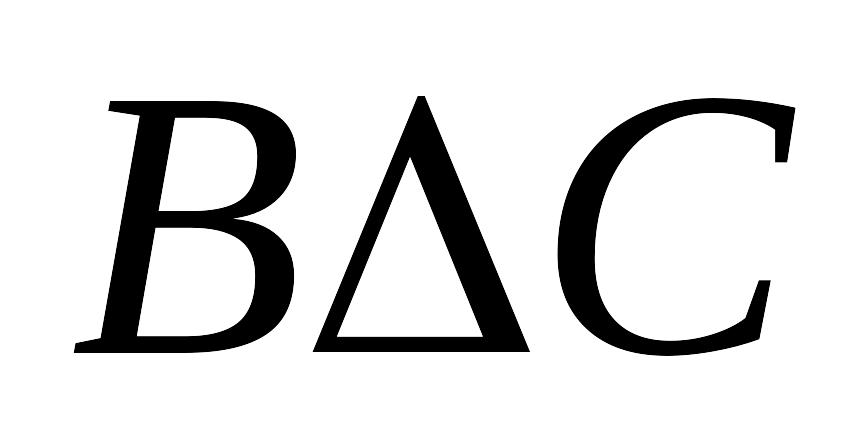
С
АВ
С
АС
ĀВ
ĀС
А
ĀВ
А
ĀС
АВС
А\

С\А
С\В
С\ Ā
С\
А\
2 . Проверьте, справедливы ли следующие равенства:
3. Изобразите на координатной плоскости декартовы произведения ав, ва, аа, вв множеств а и в:
А={a | a[0;1)}; B={b | bR и |b|2};
A={1,2,3,4,5}; B={b | b[0;3]};
A={a | aR и a21}; B={b | bR и b[3;
 )};
)};A={-1,2,-3,4,-5}; B={-4,-2,0,2,4};
А={a | a(0;3]}; B={b | bR и |b|1};
A={a | a(-;-3)}; B={1,2,3,6,7,8};
A={a | a(-;-1)}; B={b | b[3; )};
A={1}; B={b | b(0;3)};
A={a | a(-3; +)}; B={b | bR и b210};
A={1,2,3,-1,-2,-3}; B={b | bR и b327};
A={a | a(-;5]}; B={b | bR и |b|3};
A={a | a[-3;+)}; B={0,1,-1,3,-3};
A={a | a(2; +)}; B={b | bR и b38};
A={a | aR и a2+5a+60}; B={-3,-2};
A={a | a(-;-3](1;+ )}; B={b | bR и |b|<1};
A={-1,-2,-3,-4,-5}; B={b | bR и b3>27};
A={a | a(-;1)(1;+ )}; B={b | bR и b3-8};
A={a | aR и a2-3a-4=0}; B={2};
A={a | a(-2;-1] [4;+)}; B={b | bR и |b|>4};
A={a | a(-;-1,5)}; B={b | bR и 5b+116};
A={a | a(-5;-1)}; B={b | bR и b31};
A={0,2,4,6}; B={1,3,5,7};
A={a | a(-1;3]}; B={b | bR и |b|2};
A={a | aR и a2-5a+6>0}; B={0,2,4,6};
A={a | a(-;-2][2;+)}; B={b | bR и b3-2};
A=(-;+); B={b | b(0;3]};
A={a | a(-;-1)[2;+)}; B={b | bR и b2};
A={a | a(-;4)}; B={b | bR и b<14};
A={a | a(-;-3)(4;6]}; B={b | bR и 1b3<8};
A={a| aZ и -2<a3}; B=(-;+);
A={a | a[-3;-1)[1;3)}; B={b | bR и b>2};
A={a | aR и a2+5a+60}; B={b | bZ и b2+b-2=0}.
4. Запишите формулой графически заданные множества:


Тема 2-3: «Отношения и отображения»
5. Какими свойствами обладают следующие отношения? Являются ли они отношением эквивалентности, если да, то запишите классы эквивалентности и фактор-множество? Составить матрицу отношений и граф.
{(a,b) | a≤b}на множестве {5,7,9,11,13};
«быть делителем» на множестве {1,2,4,6,5,10};
«быть равным» на множестве {10,8,6,4,2};
{(a,b)| |a-b|=1} на множестве {1,2,3,4,5};
{(a,b)| 0<a-b<3} на множестве {1,2,3,4,5,6,7};
{(x,y)| x>y+1} на множестве {0,1,2,3,4,5};
{(x,y)| y<x+1} на множестве {0,-1,-2,-3,-4,-5};
{(x,y)| x<y-1} на множестве {0,-2,-4,-6,-7};
{(x,y)| y>x-1} на множестве {0,-1,-3,-5,-7};
{(a,b) | a=b2}на множестве {0,1,2,3,4,9,16};
{(a,b) | (a-b) - четное} на множестве М={1,2,3…6};
{(a,b) | (a+b) - четное} на множестве М={1,2,3…6};
{(a,b) | (a+1) – делитель (a+b)} на множестве М={1,2,3…6};
{(a,b) | a – делитель (a+b), а≠1} на множестве М={1,2,3…6};
{(a,b) | (a-b) - нечетное} на множестве М={1,2,3…6};
{(a,b) | (a+b) - нечетное} на множестве М={1,2,3…6};
{(a,b) | (b+1) – делитель (a+b)} на множестве М={1,2,3…6};
{(a,b) | b – делитель (a+b), b≠1} на множестве М={1,2,3…6};
{(a,b) | a – делитель b} на множестве М={1,2,3…6};
{(a,b) | a и b имеют общий делитель, отличный от 1} на множестве М={1,2,3…6};
{(a,b) | a и b не имеют общий делитель, отличный от 1} на множестве М={1,2,3…6};
{(a,b) | a и b имеют одинаковый остаток при делении на 3} на множестве М={1,2,3…6};
{(a,b) | a < b} на множестве М={1,2,3…6};
{(a,b) | b – делитель a} на множестве М={1,2,3…6};
{(a,b) | b=a+2}на множестве {0,1,2,3,5,6,7};
{(a,b) | b=a2}на множестве {0,1,2,4,6,8,12,16};
{(a,b) | a и b имеют одинаковый остаток при делении на 5} на множестве М={1,2,3…10};
{(a,b) | (a-b) – делитель (a+b)} на множестве М={1,2,3…6};
{(x,y)| x>y+1} на множестве {0,-1,-2,-3,-4,-5};
{(x,y)| y<x+1} на множестве {0,1,2,3,4,5};
{(x,y)| x<y-1} на множестве {0,2,4,6,7};
{(x,y)| y>x-1} на множестве {0,1,3,5,7};
