6. Способы преобразования простых суждений

1. Обращение - преобразование простого суждения путем перестановки его субъекта и предиката местами. При этом качество его не меняется, а количество может измениться.

Суждения типа А обращаются в суждения типа I. А: «Все адвокаты - юристы» - I: «Некоторые юристы - адвокаты». Исключение составляет случай, когда субъект и предикат - равнозначные понятия. В этом случае А обращается в А. А: «Все мужчины - сыновья» - А: «Все сыновья - мужчины».

Суждения типа I обращаются в суждения типа I, если субъект и предикат на­ходятся в отношении перекрещивания. I: «Некоторые спортсмены - студенты» - I: «Некоторые студенты - спортсмены». Исключение составляет случай, когда субъект и предикат находятся в отношении подчинения. В этом случае I обращается в А. I: «Некоторые юристы - адвокаты» - А: «Все адвокаты - юристы».

Суждения типа Е обращаются в суждения типа Е. Е: «Ни один кит - не рыба» - Е: «Ни одна рыба - не кит».

Частноотрицательные суждения типа О не обращаются: если мы попытаемся поменять местами субъект и предикат в суж­дении «Некоторые мужчины не есть женатые», то получится абсурдное предложение.

2. Превращение - это преобразование суждения путем введения двойного отрицания - первый раз перед связкой, а второй - перед предикатом. При этом количество не меняется, а качество меняется

А: «Все адвокаты - юристы» - Е: «Ни один адвокат не есть не юрист»;

I: «Некоторые грибы съедобные» - О: «Некоторые грибы не есть не съедобные»;

Е: «Ни один кит - не рыба» - А: «Все киты есть не рыбы»;

О: «Некоторые грибы не есть съедобные» - I: «Некоторые грибы есть несъедобные».

3. Противопоставление субъекту - это преобразование суждения путем последовательного обращения, а за­тем превращения. При этом предикатом полученного суждения, становится понятие, противопоставленное субъекту исходного суждения.

4. Противопоставление предикату - это преобразование суждения путем последовательного превращения, а затем обращения. При этом субъектом полученного суждения становится понятие, противоположное предикату исходного суждения.

7. Отношения между простыми суждениями

по логическому квадрату

Отношения между простыми суждениями по истинности принято схематически изображать в виде “логического квадрата”.

Противоположность

(контрарность)

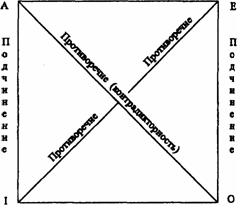
Субконтрарность

Подчинение (только по истине!) Возьмем суждение “Все слоны – млекопитающие”. Это суждение А общеутвердительное (подчиняющее). Суждение I - “Неко­торые слоны - млекопитающие” - подчиненное. Для суждений А и I, а также Е и О, находящихся в отноше­нии логического подчинения, истинность общего суждения оп­ределяет истинность частного, подчиненного суждения. Но ло­жность общего суждения оставляет частное суждение неопределенным.

Субконтрарность. В отношении частичного совпадения (субконтрарности) находятся суждения I и О, например, (I) “Некоторые свидетели дают истинные показания” и (О) “Некоторые свидетели не дают истинных показаний”. Оба они одновременно могут быть ис­тинными, но не могут быть одновременно ложными. Если одно из них ложно, то другое обязательно истинно. Но если одно из них истинно, то другое неопределенно (оно может быть либо истинным, либо ложным).

Контрарность. Отношения несовместимости: противоположность, проти­воречие. По “логическому квадрату” в отношении противополож­ности (контрарности) находятся суждения А и Е. Два суждения: (А) “Все люди трудятся добросовестно” и (Е) “Ни один человек не трудится добросовестно” - оба ложны. Но А и Е не могут быть оба истинными. Если одно из противоположных суждений истинно, то другое будет ложным. Если одно из них ложно, то другое будет неопределенно, т.к. может быть и истинным, и ложным.

Контрадикторность. В отношении противоречия (контрадикторности) находят­ся суждения А и О, а также Е и I. Два противоречащих сужде­ния не могут быть одновременно истинными и одновременно ложными. Если в настоящее время истинно суждение (I) “Неко­торые летчики - космонавты”, то ложным будет суждение (Е) “Ни один летчик не является космонавтом”.