Раздел 3 Элементы математической статистики

Тема 3.1 Вариационные ряды, их графическое изображение

Генеральная и выборочная совокупность. Выборочный метод.

Статистическое распределение. Дискретный и интервальный вариационные ряды. Полигон частот и гистограмма частот. Эмпирическая функция распределения.

Литература: [3]; [4]; [5]; [7]; [9]; [14]; [15]

Вопросы для самоконтроля

1 Генеральная и выборочная совокупность

2 Вариационный ряд. Частота вариант.

3 Статистическое распределение выборки

4 Дискретный и интервальный вариационные ряды

5 Полигон и гистограмма частот.

6 Накопленная частота. Эмпирическая функция распределения.

Краткие теоретические сведения

Математическая статистика изучает методы обработки статистических данных. Под статистическими данными понимают совокупность чисел, полученных в результате опытов, наблюдений, опросов и т.п., количественно характеризующих какой-либо признак изучаемых объектов. Множество числовых значений этого признака для всех объектов изучаемой совокупности называют генеральной совокупностью. Выборочной совокупностью (выборкой) называют множество числовых значений признака группы объектов, случайным образом отобранных из всей совокупности рассматриваемых объектов.

Наблюдаемые числовые значения признака называют вариантами, а последовательность вариант, записанных в возрастающем порядке, называют вариационным рядом. Пусть в выборке, содержащей n элементов, встречаются k разных значений (вариант) некоторого признака: Количество раз, которое наблюдалась каждая из вариант, соответственно обозначим Очевидно, что

Числа называют частотами вариант. Перечень вариант выборки с указанием соответствующих им частот называется статистическим распределением выборки.

Полигоном частот называют ломаную линию, отрезки которой соединяют точки с координатами или соответственно.

В случае, когда вариационный ряд состоит из отдельных значений признака, его называют дискретным. При большом числе вариант шкала признака разделяется на некоторое число интервалов, и вместо отдельных вариант рассматриваются группы значений вариант, попавших в последовательно расположенные интервалы. Такой вариационный ряд называют интервальным. Число m интервалов, как правило, берется в пределах от 10 до 20. Ширина интервалов h определяется путем деления размаха выборки на количество интервалов: . При этом частота интервала равна сумме частот вариант, попавших в данный интервал.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, построенных на интервалах с длиной h и высотой, равной .

Накопленной частотой называют число, которое показывает, сколько элементов выборки имеют значения, меньшие . В соответствии с этим определением можно записать:

. (62)

Эмпирической функцией распределения называется функция, определяемая следующим выражением:

(63)

Тема 3.2 Точечные и интервальные оценки параметров

распределения

Точечные оценки параметров распределения. Несмещенные, эффективные и состоятельные оценки. Генеральная средняя, выборочная средняя. Оценка генеральной средней по выборочной средней.

Генеральная дисперсия, выборочная дисперсия. Оценка генеральной дисперсии по исправленной выборочной дисперсии. Оценка среднего квадратического отклонения.

Интервальные оценки параметров распределения. Доверительная вероятность. Доверительный интервал. Распределение «хи-квадрат», Стьюдента, Фишера. Построение доверительных интервалов для оценки генеральной средней и генеральной дисперсии нормального распределения.

Литература: [4]; [5]; [6]; [7]; [9]; [12]

Вопросы для самоконтроля

1. Выборочная и генеральная средняя. Выборочная и генеральная дисперсия

2. Статистическая оценка неизвестного параметра распределения

3. Точечная оценка. Несмещенная и смещенная оценка

4. Точечная оценка генеральной средней и генеральной дисперсии

5. Интервальная оценка. Доверительный интервал

6. Интервальная оценка математического ожидания и среднего квадратического отклонения нормально распределенного признака

Краткие теоретические сведения

Числовыми характеристиками выборки являются выборочная средняя и выборочная дисперсия.

Выборочной средней выборки объема n называется среднее арифметическое всех значений :

. (64)

Аналогичным образом для генеральной совокупности объема N определяется генеральная средняя:

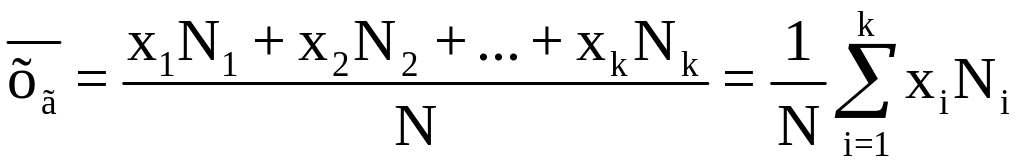. (65)

Выборочная дисперсия вычисляется по формуле:

. (66)

Аналогично определяется генеральная дисперсия :

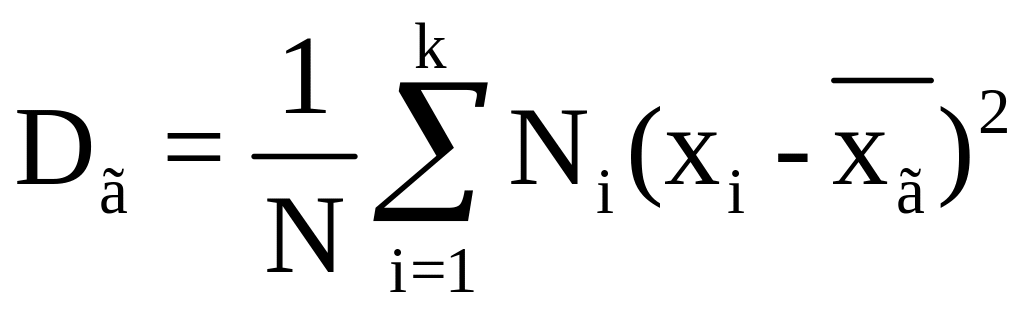. (67)

Статистической оценкой Θ* неизвестного параметра Θ теоретического распределения называют функцию Θ* = от наблюдаемых случайных величин .

Точечной называют статистическую оценку, которая определяется одним числом Θ* = , где - результаты n наблюдений над количественным признаком Х (выборка).

Несмещенной называют точечную оценку, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки. В противном случае оценка называется смещенной.

Несмещенной оценкой генеральной средней (математического ожидания) служит выборочная средняя .

Смещенной оценкой генеральной дисперсии служит выборочная дисперсия . Эта оценка является смещенной, так как

. (68)

Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия

. (69)

Интервальной называют оценку, которая определяется двумя числами – концами интервала, покрывающего оцениваемый параметр.

Доверительным называют интервал, который с заданной надежностью γ покрывает заданный параметр.

Интервальной оценкой (с надежностью γ) математического ожидания нормально распределенного количественного признака Х по выборочной средней при известном среднем квадратическом отклонении σ генеральной совокупности служит доверительный интервал

, (70)

где - точность оценки;

n – объем выборки;

t – значение аргумента функции Лапласа Ф(t), при котором

Ф(t) = γ/2; при неизвестном σ.

, (71)

где s – исправленное выборочное среднее квадратическое

отклонение;

находят по таблице по заданным n и γ.

Интервальной оценкой (с надежностью γ) среднего квадратического отклонения σ нормально распределенного количественного признака Х по исправленному выборочному среднему квадратическому отклонению s служит доверительный интервал

s(1-q) < σ < s(1+q) при q < 1 (72)

0 < σ < s(1+q) при q > 1. (73)

Список используемых источников

1 Богомолов, Н.В. Практические занятия по математике: учеб. пособие для техникумов / Н.В.Богоиолов – 3-е изд., перераб. и доп. – М.: Высш. шк., 1990.

2 Боровков, А.А. Курс теории вероятностей / А.А.Боровков. – М.: Наука, Главная редакция физико-математической литературы, 1972.

3 Валуцэ, И.И. Математика для техникумов на базе средней школы / И.И.Валуцэ, Г.Д.Дилигул. – М.: Наука, Главная редакция физико-математической литературы, 1980.

4 Гмурман, В.Е. Теория вероятностей и математическая статистика / В.Е.Гмурман. – М.: Высшая школа, 1977.

5 Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учеб. пособие для студентов вузов / В.Е. Гмурман – 9-е изд. стер. – М.: Высш. шк., 2004.

6 Гурский, Е.И. Сборник задач по теории вероятностей и математической статистике: для высш. техн. и экон. учеб. заведений / Е.И.Гурский. – 3-е изд. перераб. – Мн.: Выш. шк., 1984.

7 Гусак, А.А. Справочник по высшей математике /А.А. Гусак, Г.М. Гусак, Е.А. Бричикова. – 4-е изд. стереотип. – Мн.: ТетраСистемс, 2002.

8 Гусак, А.А. Теория вероятностей: справочное пособие к решению задач / А.А. Гусак, Е.А. Бричикова. – 3-е изд. стереотип. – Мн.: ТетраСистемс, 2002.

9 Гусак, А.А. Высшая математика. В 2-х т. Т. 2: учеб. пособие для студентов вузов / А.А.Гусак. – Мн.: ТетраСистемс, 1998.

10 Данко, П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 2: учеб. пособие для вузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – 6-е изд. – М.: Издательский дом «ОНИКС 21 век»: Мир и Образование, 2002.

11 Лисичкин, В.Т. Математика: учеб. пособие для техникумов / В.Т.Лисичкин, И.Л.Соловейчик. – М.: Высш. шк., 1991.

12 Руководство к решению задач по высшей математике: учеб. пособие. В 2 ч. Ч. 2 / Е.И.Гурский, В.П.Домашов, В.К.Кравцов, А.П.Сильванович: под общ. ред. Е.И. Гурского. – Мн.: Выш. шк.., 1990.

13 Сборник задач по высшей математике. 2 курс / К.Н.Лунгу, В.П.Нормин, Д.Т.Письменный, Ю.А.Шевченко: под ред. С.Н. Федина. – М.: Айрис-пресс, 2004.

14 Сочнев, С.В. Элементы высшей математики: сб. заданий для практ. занятий: учеб. пособие / С.В. Сочнев. – Мн.: Выш. шк., 2003.

15 Фадеев, Д.К. Элементы высшей математики для школьников / Д.К.Фадеев, М.С.Никулин, И.Ф.Соколовский. – М.: Наука, Главная редакция физико-математической литературы, 1987.

Примеры решения типовых задач