Тема 1.2 Теоремы сложения и умножения вероятностей

Теорема умножения вероятностей. Теорема сложения вероятностей несовместных событий и теорема сложения вероятностей совместных событий, следствия из них. Противоположные события, их вероятности.

Условная вероятность. Независимость событий. Теорема умножения для независимых событий.

Литература: [1]; [2]; [3]; [4]; [5]; [6]; [7]; [8]; [9]; [10]; [11]; [12]; [13]; [14]; [15]

Вопросы для самоконтроля

1 Теоремы сложения вероятностей совместных и несовместных событий

2 Вероятности противоположных событий и событий, образующих полную систему

3 Независимые события. Теорема умножения вероятностей независимых событий

4 Условная вероятность события. Теорема умножения вероятностей зависимых событий

Краткие теоретические сведения

Вероятность суммы двух несовместных событий А и В равна сумме вероятностей этих событий:

(11)

Если события образуют полную систему событий, то сумма их вероятностей равна 1. Сумма вероятностей противоположных событий также равна 1, поэтому

(12)

В общем случае вероятность суммы двух событий А и В вычисляется как

(13)

События А и В называются независимыми, если вероятность появления события А не зависит от того, произошло событие В или нет, и наоборот. Для независимых событий А и В вероятность их произведения равна произведению вероятностей этих событий:

(14)

На практике нередко вероятность события А зависит от того, произошло событие В или нет. В этом случае говорят об условной вероятности, т.е. вероятности события А при условии, что событие В произошло. Обозначают условную вероятность Р(А/В). Если события А и В являются зависимыми, то вероятность произведения этих событий

или (15)

Вероятность произведения n событий вычисляется по формуле:

(16)

В частности, для трех событий А, В и С формула принимает вид:

(17)

Тема 1.3 Формула полной вероятности. Формулы Байеса

Понятие гипотезы. Априорные вероятности гипотез. Теорема полной вероятности. Апостериорные вероятности гипотез и их расчет с помощью формул Байеса.

Литература: [1]; [2]; [3]; [4]; [5]; [6]; [7]; [8]; [9]; [10]; [11]; [12]; [13]; [14]; [15]

Вопросы для самоконтроля

1 Сущность понятия гипотезы. Априорные и апостериорные вероятности гипотез

2 Формула полной вероятности

3 Формулы Байеса

Краткие теоретические сведения

Пусть событие А может произойти только с одним из событий , ,…, , которые образуют полную группу попарно несовместных событий. События , ,…, называют гипотезами. Причем известны вероятности гипотез (i = 1, 2, …, n) и условные вероятности . Вероятность события А определяется по формуле полной вероятности:

(18)

Если произведен опыт, в результате которого произошло событие А, тогда доопытные (или априорные) вероятности гипотез должны быть заменены на новые, послеопытные (или апостериорные) вероятности , которые вычисляются по формулам Байеса:

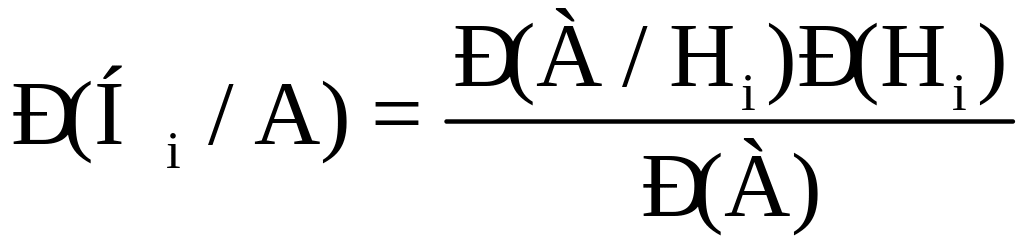, (19)

где вычисляется по формуле (18).