Ов, основанные на соотношении разноименных показателей, логически связанных друг с другом.

Относительные величины интенсивности ОВИ. Например, ВВП/численность населения=ВВП на душу населения. Например, Объем зерна/посевную площадь=сбор зерна с гектара.

ОВИ характеризуют интенсивность или эффективность изучаемых процессов, либо распространенность изучаемого явления в определенной среде. Например, показатели плотности населения. ОВИ также как абсолютные величины имеют конкретные единицы измерения – натуральные, стоимостные, или в трудовых единицах.

Относительные величины должны рассматриваться в комплексе с абсолютными величинами, в противном случае, можно прийти к неправильным выводам.

Средние величины характеризуют типичный уровень изучаемого показателя в рамках однородной совокупности. Если совокупность неоднородна, то метод СВ необходимо комбинировать с методом группировок, то есть разделить изучаемую совокупность на однородные группы, а затем по каждой группе рассчитать средние величины. Аналитическая ценность средних величин состоит в том, что они позволяют абстрагироваться от несущественных особенностей и выявить то общее, что характерно для данной совокупности в целом. Различают 2 вида средних величин: степенные средние и структурные средние. Степенные средние охватывают все единицы изучаемой совокупности, а структурные средние охватывают только часть единиц совокупности.

Степенные средние являются наиболее распространенным типом средних величин, и для их расчета используется одна формула, в которой меняется только значение степени:

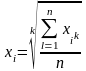, где Х_i значение признака у каждой единицы совокупности; n – число единиц совокупности, k – значение степени, которое определяет вид степенной средней, при k=2 получаем среднюю квадратическую; при k=-1 получаем среднюю гармоническое, при k=0 получаем среднюю геометрическую. Выбор степенной средней зависит, во-первых от содержания усредняемого показателя, который определяет логическую формулу расчета, во вторых от наличия исходной информации.

Все степенные средние могут быть рассчитаны в 2х вариантах, как простые средние, которые применяются обычно, если исходная информация представлена в виде первичных данных и взвешенные средние, которые применяются, если исходные данные представлены в сгруппированном виде. Х_{арифметическая простая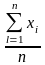}= . Эта формула применяется, если известно усредненное значение у каждого элемента совокупности или если известен общий объем этого признака.

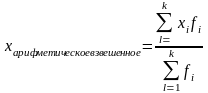
Х_i – значение усредняемого признака в группе; f_i – число единиц в совокупности в i в группе, k – число выделенных групп.

Среднее арифметическое взвешенное применяется в том случае, если исходные данные представлены в сгруппированном виде и по каждой группе известно количество единиц совокупности, или частота появления признака в группе.