4 Расчет топологии направленного ответвителя
Расчет ведем с учетом того, что переходное ослабление должно быть не менее Lно=15 дБ.
Исходя из этого, выбираем направленный ответвитель со слабой боковой связью на связанных линиях. Из величины связи между первым и вторым плечами находим эквивалентный Ксв по формуле
Принимаем условие идеального согласования
осоо=1,
где ос и ρоо - нормированные волновые сопротивления при синфазных и противофазных возбуждениях данного направленного ответвителя.
Выразим ос и ρоо во взаимосвязи с коэффициентом связи, с учетом идеального согласования
,
Отсюда
,
.
Находим волновые сопротивления для синфазной и противофазной волн по формулам
Ом,
Ом.
По графику зависимости МПЛ от размеров w/h [3] найдем соотношение s/h.
При h=1и ε=9,8 s/h=0,76 , отсюда s=0,8(мм).
Длина отрезка связных линий определяется по формуле
(мм).
Находим переходное ослабление на границе рабочей полосы частот
,
где Q- граница рабочей полосы частот.
Исследуем верхнюю границу диапазона
,
где
.
,
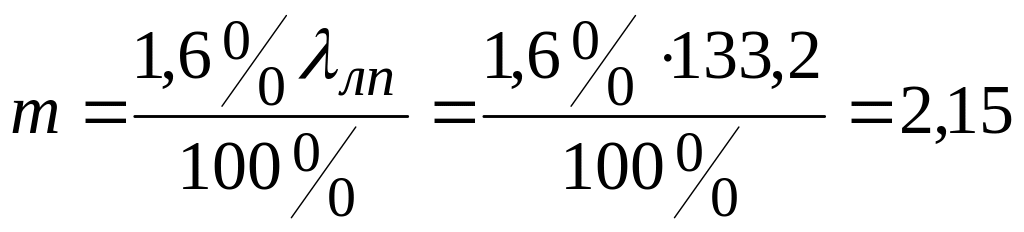дБ.
Исследуем нижнюю границу диапазона
,
дБ.
5 Расчет топологии полосно-пропускающего фильтра (ппф)
Определяем отношение для нахождения числа резонаторов ППФ
,
.
По графику [3.13, 3] определяем для данного Ω=1,99 значения Аз=30дБ, Ап,=0,406дБ, n=4.
Находим значения элементов qi из таблицы [3.4, 3] для относительной полосы прототипа
,
,
q1= q5=11,436; q2= q4=97,591; q3=137,83.
Определяем величину переходных затуханий (дБ) связанных звеньев
,
C1,5=10,94; C2,4=19,85; C3=21,42.
По данным электрического расчета определяем конструктивные размеры элементов фильтра, используя данные таблиц [3.5, 3.8, 3.10, 3].
Результаты приведены в таблице 5.1. Ширина оконечных 50 – омных полосок находится по графику [3.6, 3].
Таблица 5.1 – Геометрические размеры элементов фильтров
-
Параметры
ППФ1, ППФ2, ППФ3
b1,5/d
0,838
b2,4/d
0,985
b3/d
0,987
S1,5/d
0,340
S2,4/d
1,62
S3/d
1,90
Величину активных потерь в фильтре на средней частоте полосы пропускания можно определить по формуле
Значения элементов gi фильтра-прототипа нижних частот находим по таблице [3.1, 3] для Ап=0,4 дБ и n=4.
Величину Q0 нагруженной добротности центрального резонатора определяем по формуле
Значение QR=605 берем из графика [3.14, 10], а множитель η находим по формуле
6 Расчет топологии кольцевого делителя мощности
Простейшему
делителю мощности - тройниковому
двухканальному разветвлению на МПЛ -
присущи принципиальные недостатки:
отсутствие развязки выходных плеч,
согласование входов в узкой полосе
частот. Поэтому на практике чаще
используется двухканальный синфазный
направленный делитель мощности (рисунок
6.1), боковые плечи которого связаны
балансным резистором R
на расстоянии
от точки разветвления. Волновое
сопротивление линии кольца
,
а балластное сопротивление -
.
При таких значениях делитель имеет
следующие свойства: при согласованных
нагрузках плеч все входы делителя тоже
оказываются согласованными; мощность,
подводимая к плечу 3, делится поровну
между плечами 1 и 2 без потерь (точки Б и
В эквипотенциальны); мощность, поступающая
в плечо 1 (2) проходит в плечо 3 с ослаблением
в 3 дБ (вторая половина мощности поглощается
в резисторе R)
и не поступает в плечо 2. При подаче к
плечам 1 и 2 синфазных колебаний с равными
амплитудами делитель будет работать
как сумматор без потерь.
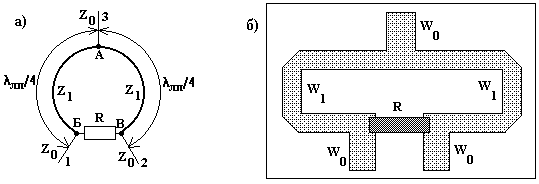
Рисунок 6.1 - Кольцевой делитель мощности:
а) структурная схема; б) возможная топология.
Кольцевой
делитель работает в широкой полосе
частот. В частности,
дБ и
обеспечиваются в 36% полосе частот [14].
Активные потери в кольцевой линии
незначительно ухудшают параметры
делителя. Проектирование кольцевого
делителя сводится к проектированию
отрезков МПЛ определенной длины и
волнового сопротивления, а также
пленочного резистора.
Для расчета размеров делителя мощности с равным делением необходимо определить волновое сопротивление соединительных линий по формуле
,
Активное сопротивление нагрузки определяется по формуле
,
.
Радиус кольцевого участка, образованного двумя четвертьволновыми отрезками, находится следующим образом
,
