Тема 2. Векторные аналоги теоретико-множественных моделей для построения диагнозов

Вновь обратимся к последовательности логических сетей, полагая, что — элементарная логическая сеть.

Пусть построены эквивалентные прямая и обратная модели и логической сети , и логическая сеть в последовательности сетей получена из предыдущей замещением входного элемента. Заменим каждый вектор из , а также каждый вектор из группой векторов, включающей, в зависимости от значения компоненты , соответствующей замещаемому входному элементу, следующие векторы:

а) если — единственный вектор, содержащий вместо п компонент 0, соответствующих новым входам;

б) если (или ) — все векторы, отличающиеся от данного тем, что вместо имеется п компонент, соответствующих новым входам; значения этих компонент образуют вектор из эквивалентной прямой (или обратной) диагностической модели подключаемой элементарной логической сети.

Рассмотрим теперь случай, когда логическая сеть получена из предыдущей логической сети , для которой уже построены прямая и обратная эквивалентные модели и отождествлением входов. Для получения эквивалентных прямой и обратной моделей логической сети заменим каждый вектор имеющихся моделей и , группой векторов, которая включает, в зависимости от набора значений соответствующих отождествляемым входам сети компонент данного вектора, следующие векторы:

а) если — единственный вектор с дополнительной соответствующей новому входу компонентой со значением ;

б) если = ... = = (или = ), = ... = = — единственный вектор с дополнительной соответствующей новому входу компонентой со значением (или ) и отличающийся от данного вектора еще и тем, что = ... = = (или = 0);

в) если =...= = , =...= = , =...= = , l <r<= t — два вектора с дополнительной соответствующей новому входу компонентой со значениями или и отличающиеся еще и тем, что в первом из них = ...= = 0, = ... = = , а во втором = ... = = , =…= = 1.

Далее для завершения построения моделей и логической сети ( , ) необходимо над построенными совокупностями векторов выполнить операции включения и поглощения; при этом следует рассматривать сопряжения только векторов из совокупности в) и только по новой компоненте j.

Наряду с эквивалентными моделями , находят применение и соответствующие эквивалентные модели _, . По построению они отличаются тем, что при вычислении моделей логической сети ( , ), полученной отождествлением входов, не выполняются операции сопряжения, если получающийся при соединении вход является входом логической сети (S, ). Можно показать, что эти модели также покрывают множества изменений эталонной логической сети, содержащие для каждой сети из множеств , соответственно эквивалентного представителя. Эти более простые модели достаточны для построения диагнозов. Для построения тестов необходимы более сложные модели _{, .}

Пример. Построим эквивалентную прямую диагностическую модель логической сети на рис. 3.

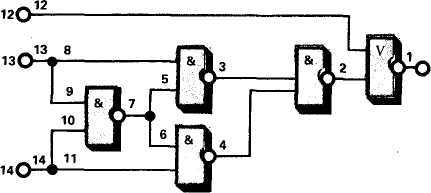
Рис. 3

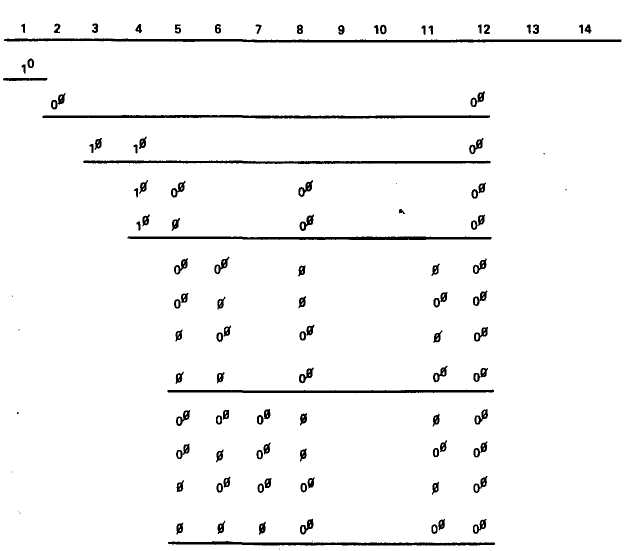
Продолжение

Аналогично можно построить обратную модель

По построению эквивалентные прямая и обратная модели представляют собой описания диагнозов логической сети, соответствующих минимальной информации о ее функционировании, когда известно лишь единственное значение выхода логической сети (1 в первом и 0 во втором случае). Уточнение информации о функционировании логической сети позволяет уточнить диагноз. Один из способов уточнения приводит к понятию -компоненты диагностической модели.

Пусть известно, что значение выхода логической сети есть 1 (или 0), а также то, что набор значений входных сигналов при этом принадлежит грани ( ,..., ,..., ) . Это возможно, если логическая сеть принадлежит множеству (или ) логических сетей. Эквивалентное покрытие (или ) этого множества можно получить из покрытия (или ), заменив во всех векторах компоненты , соответствующие входным элементам компонентами по следующему правилу:

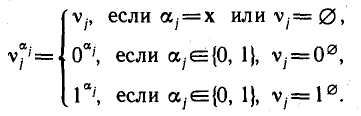
Таким образом, = (х, ...х), = (х, ..., х).

Покрытия , получаемые из описанным способом, называются -компонентами эквивалентных прямой и обратной диагностических моделей и . Аналогично определяются и -компоненты модели и , рассмотренных в предыдущем параграфе.

Если известны результаты нескольких экспериментов такого рода, т. е. результат сложного эксперимента

где — грани n-мерного куба, которым принадлежат входные наборы в отдельных простых экспериментах, — соответствующие значения выхода, то эквивалентное покрытие множества логических сетей, удовлетворяющих этому сложному эксперименту, можно получить векторным пересечением ос-компонент соответствующих эквивалентных моделей.

Построение диагнозов по данным об экспериментах при достаточно большом числе векторов в моделях и требует выполнения большого числа операций векторного пересечения. В связи с этим рассмотрим один способ предварительного упрощения моделей по известному описанию эксперимента, предложенный Л. И. Ляшенко.

Заметим, что каждому вектору , из (или ) соответствует грань единичного n-мерного куба такая, что на любом наборе из функция каждой логической сети из множества, соответствующего вектору , имеет значение 1 (или 0). Соответствующие входам п - s + 1, …, n - s + j,..., s компоненты , j= 1, .... п вектора можно получить по правилу

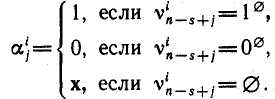
Например, векторам моделей и логической сети на рис. 26, рассмотренным в предыдущем параграфе, соответствуют следующие грани:

а) (0, 1, 1), (0, 1, 1), (0, 1, 0), (0, 1, 1), (0, 0, 1), (0, 0, 0),

б) (1, х, х), (х, 1, х), (х, 0, 1), (х, 1, 0), (х, х, 1), (х, 0, х), (х, х, 0).

Подмеченная особенность моделей позволяет в некоторых случаях по известному описанию эксперимента удалить до начала вычислений диагноза некоторые векторы моделей, соответствующие изменениям логической сети, заведомо не удовлетворяющим данному конкретному эксперименту. Действительно, пусть грань соответствует в указанном смысле вектору , и в описании эксперимента имеется пара ( , 0), причем . Ясно, что все логические сети из множества, соответствующего вектору , в этом случае не удовлетворяют эксперименту ( , 0), а следовательно, и эксперименту в целом и могут быть удалены до начала вычислений.

Пример. Рассмотрим эксперимент

{((0, 0, 0), 1), ((0, 0, 1),0), ((0, 1, 0), 0), ((0, 1, 1),1), ((1, 0, 0), 0)}

с логической сетью на рис. 26. Могут быть удалены третий и пятый векторы из , второй, пятый, шестой и седьмой векторы из

Обозначим и множества остающихся векторов из и , и — множества соответствующих векторов из и _.

Пример. Построим диагноз, соответствующий рассмотренному выше эксперименту.

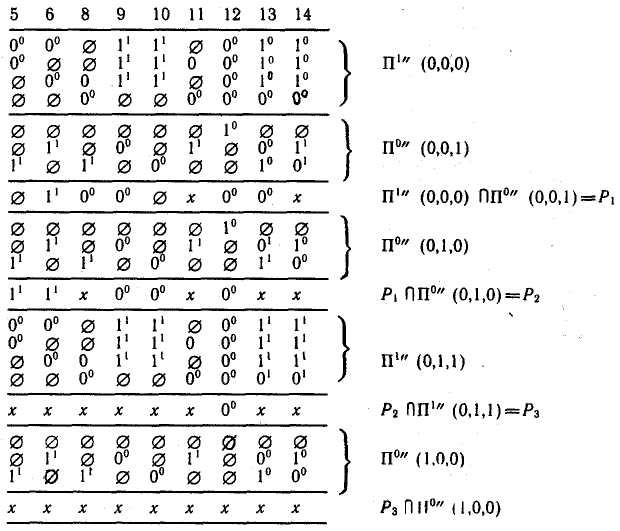
Полученный диагноз включает единственную эталонную логическую сеть, т. е. при рассмотренной реакции на входные наборы данного эксперимента гарантируется отсутствие любой неисправности из класса в данной логической сети.

"Неразрушающий контроль в производстве" –

Оценка точности и настроенности технологической операции по результатам визуального выборочного контроля деталей методом группировки. Определение границ сортировки и номинальных размеров калибров распределения для контролируемого размера детали. Определение коэффициентов точности и настроенности, а также прогнозируемого и фактического уровня брака.

Анализ системы контроля качества как системы массового обслуживания (СМО) с отказами и простейшими потоками заявок. Оценка характеристик эффективности функционирования СМО.

Анализ системы контроля качества как СМО с неограниченной или ограниченной очередью и простейшими потоками заявок. Оценка характеристик эффективности функционирования СМО.

Неразрушающий акустический контроль упругих свойств материалов. Расчёт модуля нормальной упругости, модуля сдвига и коэффициента Пуассона при известных скоростях продольной и поперечной составляющих акустических волн, найденных в ходе неразрушающего контроля образца материала.

Неразрушающий акустический контроль механической прочности материалов. Расчёт предела прочности при известной скорости акустических волн, найденных в ходе неразрушающего выборочного контроля образцов материала.

Неразрушающий статистический контроль с применением контрольных карт по количественному признаку. Определение границ регулирования для контрольных карт. Определение налаженности техпроцесса и доли брака в техпроцессе на основе сравнения поля допуска и границ регулирования для контрольных карт индивидуальных значений контролируемого параметра. Определение достоверности контроля на основе оперативных характеристик для контрольных карт средних и карт размаха.