- •Обзорные лекции к государственному экзамену "Физические основы получения информации"
- •1. Прохождение ультразвуковой волны через границу раздела двух сред
- •2. Коэффициенты прозрачности и отражения
- •3. Влияние тонкого слоя на прохождение волн
- •4. Основные параметры звукового поля
- •"Методы контроля и управления качеством"
- •"Методы технической диагностики"
- •Тема 1. Построение векторного представления функции неисправности, не прибегая к ее табличному представлению
- •Тема 2. Векторные аналоги теоретико-множественных моделей для построения диагнозов
- •"Теория физических полей"
- •1 Синтез микрополосковой линии передач (мпл)
- •2 Расчет топологии свч переключателя
- •3 Расчет топологии балансного смесителя
- •4 Расчет топологии направленного ответвителя
- •5 Расчет топологии полосно-пропускающего фильтра (ппф)
- •6 Расчет топологии кольцевого делителя мощности
- •7 Расчет управляемого аттенюатора
- •"Физические методы контроля"
- •Активные акустические методы
- •3. Классификация преобразователей
- •4. Обозначение преобразователей
- •6. Расчет режимов намагничивания
- •Расчёт силы тока для циркулярного намагничивания
- •Расчёт силы тока для продольного намагничивания
- •Пример расчёта режимов намагничивания
- •"Измерительные информационные системы"
- •"Конструирование электронных кип"
- •Расчет размерных цепей
- •1.2.4 Допуск замыкающего звена.
- •1.2.5 Предельные отклонения составляющих звеньев.
- •2 Расчёт механических характеристик пластинчатых конструкций
- •3 Помехоустойчивость узлов
- •3.1 Паразитные связи на печатных платах
- •"Технология электронных кип" Проектирование однопредметной поточной линии
- •Проектирование многопредметной поточной станции.
- •Методы обеспечения сборочных поточно-конвейерных линий комплектующими изделиями.
"Методы технической диагностики"
Тема 1. Построение векторного представления функции неисправности, не прибегая к ее табличному представлению
Алгоритм вычисления покрытия множества наборов, на которых проявляется рассматриваемая константная неисправность входных элементов, имеет следующий вид:
1.
Построить покрытия
![]() и
и
![]() областей нулевых и единичных значений
функции
областей нулевых и единичных значений
функции
![]() эталонной
сети. Для построения каждого покрытия
использовать следующий алгоритм:
эталонной
сети. Для построения каждого покрытия
использовать следующий алгоритм:
Пусть
построено покрытие
![]() для логической сети
для логической сети
![]() ,
и логическая сеть
,
и логическая сеть
![]() получена из нее замещением входного
элемента j.
Тогда покрытие
получена из нее замещением входного
элемента j.
Тогда покрытие
![]() для
логической сети
для
логической сети
![]() получим, заменив каждый вектор исходного
покрытия совокупностью векторов. В
новых векторах вместо элемента
получим, заменив каждый вектор исходного
покрытия совокупностью векторов. В
новых векторах вместо элемента
![]() ,
соответствующего замещаемому входному
элементу, имеется группа элементов (по
числу входов подключаемой логической
сети). Они имеют значения х, если значение
заменяемого элемента есть х, или значения,
образующие различные векторы из
сокращенного покрытия области нулевых
(при значении 0 заменяемого элемента)
или единичных значений функции
подключаемой логической сети.
,
соответствующего замещаемому входному
элементу, имеется группа элементов (по
числу входов подключаемой логической
сети). Они имеют значения х, если значение
заменяемого элемента есть х, или значения,
образующие различные векторы из
сокращенного покрытия области нулевых
(при значении 0 заменяемого элемента)
или единичных значений функции
подключаемой логической сети.
Если
же логическая сеть
![]() получена
из логической сети
получена
из логической сети
![]() отождествлением некоторых входов, то
покрытие
отождествлением некоторых входов, то
покрытие
![]() для
логической сети
для
логической сети
![]() получим,
удалив из исходного покрытия векторы,
в которых некоторым отождествляемым
входам соответствуют как значения 1,
так и значения 0; в остающихся векторах
добавляется один элемент, соответствующий
новому входу. Он имеет значение х, если
значение х имеют все элементы исходного
вектора, соответствующие отождествляемым
входам, или значение 0 или 1, если хотя
бы один из них имеет значение 0 или 1.
После этого все элементы векторов,
соответствующие отождествляемым входам,
удаляются, выполняются операции
сопряжения по новому элементу, затем
операции включения образованных при
этом векторов и операции поглощения.
получим,
удалив из исходного покрытия векторы,
в которых некоторым отождествляемым
входам соответствуют как значения 1,
так и значения 0; в остающихся векторах
добавляется один элемент, соответствующий
новому входу. Он имеет значение х, если
значение х имеют все элементы исходного
вектора, соответствующие отождествляемым
входам, или значение 0 или 1, если хотя
бы один из них имеет значение 0 или 1.
После этого все элементы векторов,
соответствующие отождествляемым входам,
удаляются, выполняются операции
сопряжения по новому элементу, затем
операции включения образованных при
этом векторов и операции поглощения.
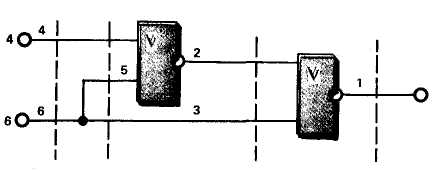
Рис. 1
Пример.
Для логической сети на рис. 1
последовательность сетей включает
четыре логические сети, соответствующие
пунктирным линиям. Процессы построения
двух сокращенных покрытий
![]() и
и
![]() представляются следующим образом. (В
квадратных скобках указаны значения
компонентов, замещаемых при переходе
к очередной подсети, в круглых скобках
— ранее замещенные компоненты.)
представляются следующим образом. (В
квадратных скобках указаны значения
компонентов, замещаемых при переходе
к очередной подсети, в круглых скобках
— ранее замещенные компоненты.)
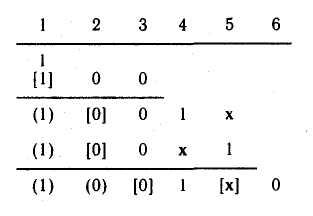

В итоге получено
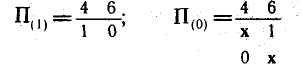
2.
Разбить множества
![]() и
и
![]() граней на пары множеств
граней на пары множеств
![]() ,
,
![]() и
и
![]() ,
,
![]() .
Множества
и
включают
грани из
и
,
имеющие непустые пересечения с гранью
.
Множества
и
включают
грани из
и
,
имеющие непустые пересечения с гранью
![]() множества
и
—
остальные грани из
и
соответственно.
множества
и
—
остальные грани из
и
соответственно.
3.
В векторных обозначениях граней из
покрытий
и
заменить
значения компонент, соответствующих
неисправным входным элементам, значениями
х.
Обозначим полученные покрытия
![]() и
и
![]() .
.
4. Искомое покрытие образуется гранями, являющимися пересечениями граней из с гранями из и граней из с гранями из .
Полученное покрытие в общем случае не является сокращенным.
Пример.
Вычислим множество входных наборов,
при которых проявляется неисправность
![]() логической
сети на рис. 2.
логической
сети на рис. 2.
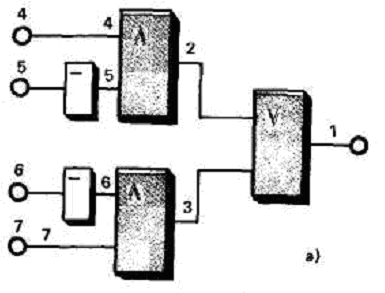
Рис. 2
1. Образуем покрытия областей единичных и нулевых значений функции исправной логической сети:
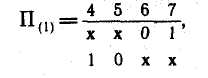
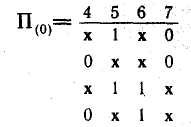
2.
Неисправности
![]() соответствует вектор (грань)
соответствует вектор (грань)
![]()
Образуем множества
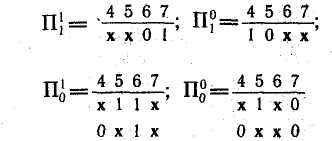
3. Образуем покрытия
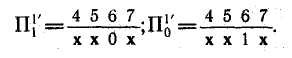
4. Построим искомое покрытие