Обзорные лекции к государственному экзамену "Физические основы получения информации"

1. Прохождение ультразвуковой волны через границу раздела двух сред

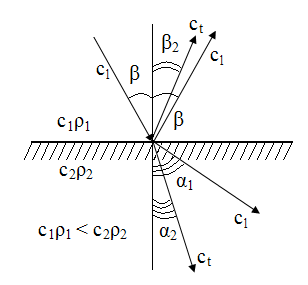
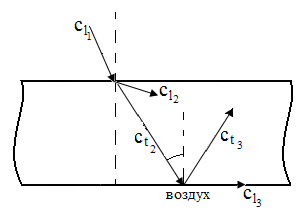
При падении продольной волны с_l под углом β из одной среды в другую происходит отражение, преломление и трансформация волны и в общем случае возникают еще 4 волны:

- преломленные: продольная и поперечная;

- отраженные: продольная и поперечная.

Направление распространения отраженных и преломленных волн отличаются от направления падающей волны, однако все эти направления лежат в одной плоскости – плоскости падения. Плоскость падения – плоскость, образованная падающим лучом и нормалью к отраженной поверхности, восстановленной в точку падения луча.

Углы отражения и преломления можно рассчитать исходя из следующих соображений:

DA – фронт падающей волны;

BK – фронт отраженной волны;

BC – фронт преломленной волны.

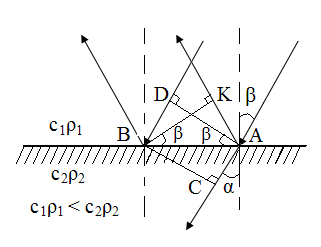
Рассмотрим три треугольника: Δ BDA, Δ BKA, Δ BCA. Выразим в каждом треугольнике сторону АВ.

Δ BDA: Δ BCA: Δ BKA:

- выражение Снеллиуса

1. Первый критический угол

Угол падения продольной волны, при котором трансформируемая продольная волна во второй среде сливается с границей раздела сред, называется первым критическим углом (β_Iкр). Для пары оргстекло - сталь β_Iкр = 27,5⁰.

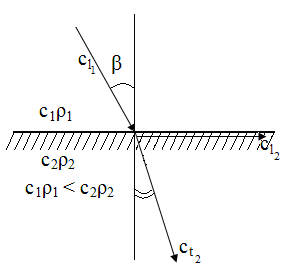
2. Второй критический угол

Второй критический угол – это угол падения продольной волны, при котором угол преломления поперечной волны равен 90⁰. Это волна называется поверхностной волной Релея. Для пары оргстекло - сталь β_IIкр = 57⁰.

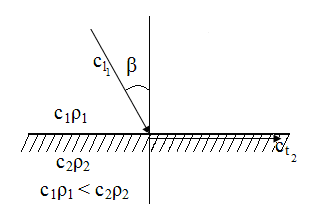
3. Третий критический угол

На границу металл-воздух падает трансформированная поперечная волна и третьим критическим углом называется такой угол, при котором угол отражения продольной волны равен 90⁰. Для стали β_IIIкр = 33⁰.

2. Коэффициенты прозрачности и отражения

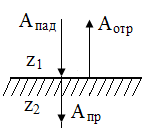
Плоская продольная волна падает перпендикулярно поверхности раздела двух сред с различными акустическими сопротивлениями. Часть волны отражается, а часть проходит.

Амплитуды волн выражаются через:

А_от = R*А_пад, где R - коэффициент отражения;

А_пр = D*А_пад, где D – коэффициент прозрачности;

Интенсивности волн:

J_пад = J_отр + J_пр

Из закона сохранения энергии следует, что интенсивность падающей волны равна интенсивности отраженной и прошедшей волн. На границе раздела двух сред должно выполняться условие непрерывности: давление и скорость не должны испытывать скачков. Смещение точки в преломленной волне есть алгебраическая сумма смещений, вызванных падающей и отраженной волнами.

Подставляем во второе уравнение системы значение интенсивности через амплитуду:

, где - коэффициент отражения по амплитуде

, где - коэффициент прозрачности по амплитуде

- коэффициент отражения по энергии

- коэффициент прозрачности по энергии

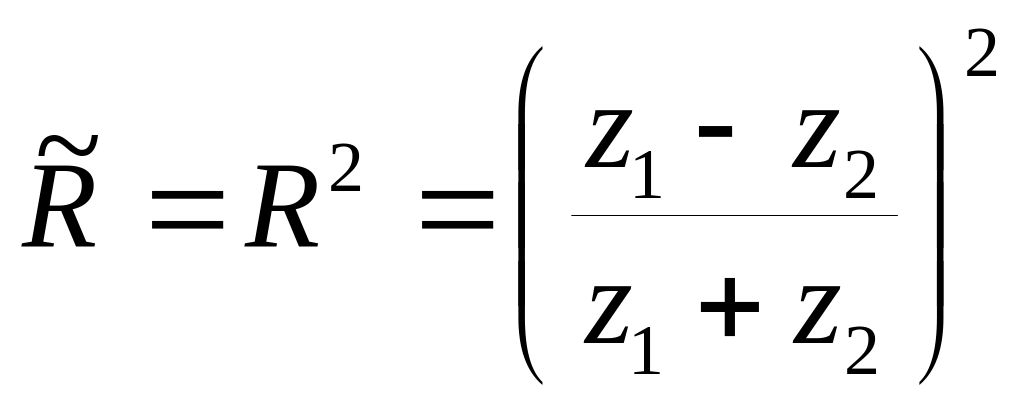
3. Влияние тонкого слоя на прохождение волн

Очень тонкий промежуточный слой слабо влияет на коэффициент отражения или прозрачности, если его длина много меньше четверти длины волны λ слоя. Если толщина слоя равна λ/2, то коэффициент отражения стремиться к нулю.

Коэффициент прозрачности и отражения для наклонно падающей волны.

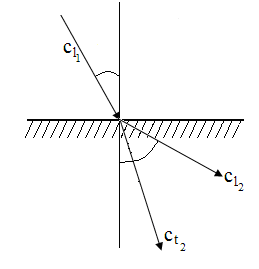
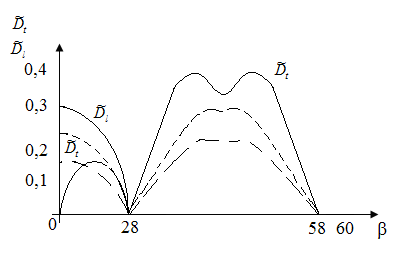
Зависимость коэффициента прозрачности от угла падения продольной волны на границе оргстекло-сталь (для идеального случая).