
2. По построенным в задаче 1 рядам распределения рассчитать:
а) размах вариации;
б) среднее линейное отклонение;
в) среднее квадратичное отклонение;
г) коэффициент вариации.
Проанализировать полученные результаты.
Решение:
Для расчета показателей вариации используем расчетные данные, представленные в таблицах 2 и 3.
1) Размах вариации представляет собой абсолютную разность между максимальным и минимальным значениями признака в изучаемой совокупности:
а)![]() R
= xmax
– xmin
= 43,17 – 1,21 = 41,96 млн. руб.
R
= xmax
– xmin
= 43,17 – 1,21 = 41,96 млн. руб.
б) R = xmax – xmin = 11 – 5 = 6 лет
2) Среднее линейное отклонение:
а)
![]()
б)
![]()
3) Дисперсия:
а)

б)
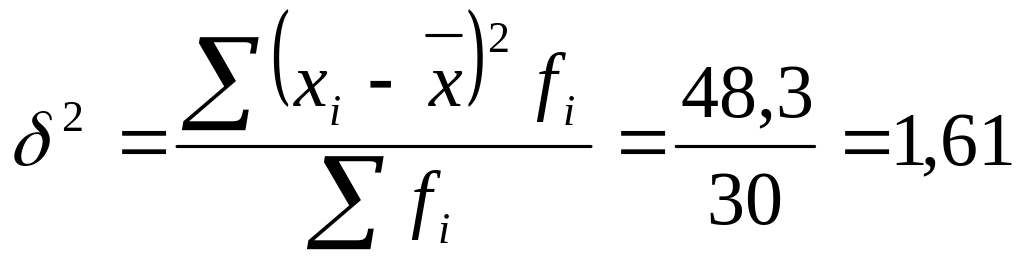
4) Среднее квадратичное отклонение вычисляется как корень квадратный из дисперсии:
а)
![]()
б)
![]()
5) Коэффициент вариации – это относительный показатель вариации, равный процентному отношению среднего квадратического отклонения к средней арифметической:
а)
![]()
б)
![]()
Вывод: рассчитанная величина коэффициента вариации для распределения банков по величине капитала свидетельствует о значительном уровне колебаний признака (т.к. рассчитанный коэффициент имеет значение значительно более 33%). Данная совокупность считается неоднородной. Коэффициент вариации для распределения банков по возрастам не превышает 33 %. Данная совокупность является однородной.
Задача № 2
По данным задачи 1 провести 20-процентную механическую выборку банков по величине капитала. Результаты представить в таблице.
Установить:
а) средний размер капитала банков по выборке;
б) величину ошибки при определении величины капитала на основе выборки;
в) вероятные пределы колебания величины капитала для всех банков при вероятности 0,954.
Решение:
Таблица 8
№ группы |
Группы банков по величине капитала, млн. руб. |
Число банков, fi |
Середина интервала xi |
xi * fi |
Сумма накопленных частот, S |
xi – |
|xi - | * fi |
(xi – )2 |
(xi – )2 *fi |
1 |
8,20-15,20 |
1 |
11,700 |
11,70 |
1 |
-12,820 |
12,820 |
164,352 |
164,352 |
2 |
15,20-22,19 |
2 |
18,695 |
37,39 |
3 |
-5,825 |
11,650 |
33,931 |
67,862 |
3 |
22,19-29,18 |
1 |
25,685 |
25,69 |
4 |
1,165 |
1,165 |
1,357 |
1,357 |
4 |
29,18-36,18 |
1 |
32,680 |
32,68 |
5 |
8,160 |
8,160 |
66,586 |
66,586 |
5 |
36,18-43,17 |
1 |
39,675 |
39,68 |
6 |
15,155 |
15,155 |
229,674 |
229,674 |
|
ВСЕГО |
6 |
- |
147,14 |
- |
- |
48,950 |
- |
529,831 |
а) Средний размер капитала банка по выборке:
![]()
б) Средняя ошибка выборки:
μх
=
![]() ,
,
где n - число единиц выборки (n = 30*0,2 = 6); N- число единиц генеральной совокупности, N = 30.
Дисперсия :
![]()
μх
=
![]() =
=
![]()
Предельная ошибка выборки:
при заданной вероятности р = 0,954 коэффициент доверия t = 2
![]()
в) Вероятные пределы колебания величины капитала:
![]()
![]()
![]()
