Теор.Вейштрассе: если возрастающая последовательность xn ограничена сверху, то она сходится, аналогично с убыванием.

Теор.Бальцано-Вейштрассе: из всякой ограниченной последовательности можно выделить сходящуюся последовательность.

Следствие: 1-любое бесконечное подмножество ограниченной последовательности имеет частичный предел. 2-Если все частные пределы последовательности равны, то она сходится к этому числу(а).

Критерий Коши сходимости последовательности:

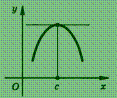
Теорема Ферма.  Если функция у = f (х),  определенная в интервале (а ; b), достигает в  некоторой точке с этого интервала наибольшего (или наименьшего) значения и существует  производная f ′(с), то f ′(с) = 0.  

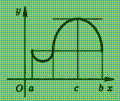
Геометрический смысл этой теоремы состоит в том, что касательная к графику функции у = f (х) в точке с абсциссой спараллельна оси абсцисс (рис.).    Теорема Ролля. Если функция у = f (х),  непрерывная на отрезке [а ; b] и  дифференцируемая в интервале (а ; b), принимает на концах этого отрезка равные значения f (a) = f (b), то в интервале (а ; b) существует такая точка с, что f ′(с) = 0.  Геометрически эта теорема означает  следующее: если крайние ординаты кривой у = f (х) равны, то на кривой найдется точка, в которой касательная параллельна оси абсцисс (рис.).    Теорема Лагранжа. Если функция у = f (х) непрерывна на отрезке [а ; b] и  дифференцируема в интервале (а ; b), то в этом интервале найдется такая точка с, что   

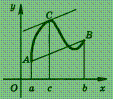
Эта теорема имеет простой геометрический смысл (рис.): на графике функции у = f (х)  между точками А и В найдется такая внутренняя точка С, что касательная к графику в точке С параллельна хорде АВ.

   

Следствие. Если f ′(x) = 0 в интервале (а ; b), то в этом интервале функция f (х) постоянна.  

Теорема Коши. Если функции f (х) и g (х): 1) непрерывны на отрезке [а ; b];  

2)  дифференцируемы в интервале (а ; b);  

3) g'(x) ≠ 0 в этом  интервале,  

то в интервале (а ; b) существует  такая точка с, что имеет место равенство 

 

Предел последовательности

Число а наз. пределом послед. {x_n}, если для >0  N_ такой, что при всех n>N_ выполнено нер-во |x_n-а|<.

Подпоследовательностью x_n назыв. числовая последовательность, которая составлена из членов последовательности x_n и в которой порядок следования её элементов совпадает с их порядком следования в исходной последовательности x_n.

Послед. наз. сходящейся, если она имеет предел, и расходящейся­­ – если не имеет.

Частичным пределом последовательности называется предел какой-либо её подпоследовательности, если существует хотя бы одна подпоследовательность, имеющая предел.

#2 Критерий Коши. Для того чтобы пос-ть

{x_n}nN имела предел, необходимо и

достаточно, чтобы для любого >0 существовал

номер N() такой, что при n,m>N() выполняется

неравенство |x_n - x _m| < 

Теорема о пределе промеж. послед.

Если lim_nx_n=a, lim_nz_n=a и справедливо нер-во x_n<=y_n<=z_n, то lim_ny_n=a.Д-во: дост. док-ть, что послед. {y_n-a} явл. б.м. Обозначим через N номер, начиная с которого, вып. нер-ва из условия. Тогда начиная с этого номера, будут выполняться также нер-ва x_n-a<=y_n-a<=z_n-a. Отсюда следует, что при n>N эл-ты послед. {y_n-a} удовл. нер-ву: |y_n-a| <= max{ |x_n-a| , |z_n-a| }

Св-ва сходящихся посл-тей

1. Теорема «Об единственности пределов»:

Если посл-ть xn сходится, то она имеет единственный предел.

Доказательство. Предположим, что два вещественных числа а и b являются пределами сходящейся последовательности {xn}. xn=a+an и xn=b+bn, где {an} и {bn} - некоторые бесконечно малые последовательности. Получим an−bn=b−a . Последовательность {an−bn}  является бесконечно малой, а в силу равенства an−bn=b−a  все элементы этой бесконечно малой последовательности равны одному и тому же вещественному числуb−a . Число b−a  равно нулю, т. е. b=a.

2. Теорема «Сходящаяся посл-ть ограничена»

Доказательство. Пусть {xn} - сходящаяся последовательность и a ее предел. Фиксируем некоторое положительное число ε и по нему номер N такой, что ∣xn−a∣<ε  при n≥N  или, a−ε<xn<a+ε при n≥N Обозначим через A наибольшее из следующих (N+1) чисел: ∣a−ε∣,∣a+ε∣,∣ ∣  x1∣ ∣  ,∣ ∣  x2∣ ∣  ,...,∣ ∣  хN−1∣ ∣   .Тогда, очевидно, ∣xn∣≤A  для всех номеров n, а это и доказывает ограниченность последовательности {xn}.

3. Теорема «Об арифметических действиях»:

а) предел lim(n)(xnyn)=ab

б) предел lim(n)(xnyn)=ab

в) предел lim(n)(xn/yn)=a/b, b0

4. Теорема «О сходимости монотон. посл-ти»

Всякая монотонная посл-ть явл-ся сходящейся,

т.е. имеет пределы.

#3 Определение предела по Коши. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого ε > 0 существует δ > 0 такое, что для всех x, удовлетворяющих условию |x – a| < δ, x ≠ a, выполняется неравенство |f (x) – A| < ε.

Определение предела по Гейне. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для любой последовательности   такой, что   сходящейся к числу a, соответствующая последовательность значений функции   сходится к числу A.

Т-ма о пределе промеж. ф-ции

 Если функция ƒ(х) заключена между двумя функциями φ(х) и g(х), стремящимися к одному и тому же пределу, то она также стремится к этому пределу, т. е. если то Доказательство: Из равенств (17.6) вытекает, что для любого ε>0 существуют две окрестности δ₁ и δ₂ точки х_о, в одной из которых выполняется неравенство |φ(х)-А|<ε, т. е.

 -ε<φ(х)-А<ε,                                 (17.8)

а в другой |g(х)-А|<ε, т. е.

-ε<g(х)-А<ε.                                        (17.9)

 Пусть δ — меньшее из чисел δ1 и δ2. Тогда в δ-окрестности точки x0 выполняются оба неравенства (17.8) и (17.9). Из неравенств (17.7) находим, что φ(x)-A≤f(x)-A≤g(x)-A  (17.10)

С учетом неравенств (17.8) и (17.9) из неравенства (17.10) следуют неравенства -ε<ƒ(х)-А<ε или |ƒ(х)-А|<ε. Мы доказали, что для всех ε>0 существует δ>0 и для всех x: 0<|х-х0|<δ и |ƒ(х)-А|<ε, то есть lim ƒ(х)=А при х –> x0.

1-й замечательный предел

lim(x0) sinx/x =1

#4 Бесконечно малые функции

Ф-ция (х) наз-ся б/м если ее предел в этой т-ке

равен 0 из этого определения вытекает

следующее св-во б/м ф-ций:

а) Алгебраическая сумма и произведение

б/м ф- ций есть б/м ф-ции.

б) Произведение б/м ф-ции на ограниченную ф-

цию есть б/м ф-ция, т.е. если (х)0 при хх0,

а f(x) определена и ограничена ( С:(х)С)=>

(х)*(х)0 при хх0

Теорема о связи Б.Б.Ф. и Б.М.Ф.

Если (x)-бмф(0), то ф-ция 1/(x)-ббф и наоборот.

Д-во: пусть (x) – бмф при x  x₀, т.е. lim_xx0(x)=0. Тогда

(>0 >0 x: 0< |x-x₀| <  |(x)|< ),

т.е. |1/(x)|>1/(=М).

#5. Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞) есть бесконечно малая функция. Док-во: Так как функция f(x) ограничена, то существует число М такое, что при всех значениях x из некоторой окрестности точки a |f(x)|≤M. Кроме того, так как a(x) – бесконечно малая функция при x→a, то для произвольного ε>0 найдется окрестность точки a, в которой будет выполняться неравенство |α(x)|< ε/M. Тогда в меньшей из этих окрестностей имеем |αf|< ε/M= ε. А это и значит, что af – бесконечно малая. Для случая x→∞ доказательство проводится аналогично. Из доказанной теоремы вытекают:

Следствие 1. Если  и  , то  .

Следствие 2. Если  и c=const, то  .

#6 Т. о втором замечательном пределе:

lim(n)(1+1/n)^n=e (1)

lim(n0)(1+x)^1/x=e (2)

Для раскрытия неопределённостей видов  ,  ,   пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.

#7 Сравнение роста Б.м.:

Определения. Пусть при   функции f(x) и g(x) являются бесконечно малыми. Тогда:

1. Если   , то f(x) называется бесконечно малой высшего порядка относительно g(x).

2. Если   (конечен и отличен от 0), то f(x) называется бесконечно малой n-го порядка относительно g(x).

3. Если   , то f(x) и g(x) называются эквивалентными бесконечно малыми.Эквивалентность записывается так:   .

Основные эквивалентности:

sinxx tgxx arcsinxx arstgxx 1-cosxx²/2

e^x-1x a^x-1xlna ln(1+x)x (1+x)ⁿ-1nx

Доказательство эквивалентности б/м отдельно в приложении к документу!

#8 Т. о разности эквивалентных Б.м.: Разность двух эквивалентных бесконечно малых функций есть бесконечно малая более высокого порядка, чем каждая из них.

Справедливо и обратное утверждение: если разность б.м.ф. α и ß есть бесконечно малая высшего порядка, чем α или ß, то α и ß — эквивалентные бесконечно малые. Действительно, так как

  т. е.    Отсюда     т. е. α~ß. Аналогично,   если  то α~ß.

Т. о замене эквивалентных в пределе отношения:

(x)1(x); (x)1(x)lim(xa)(x)/(x)= lim(xa)1(x)/1(x) при xa

#9 Непрерывность ф-ции в точке

Ф-ция y = f(x) наз. непрерывной в точке x₀, если существует предел ф-ции в этой точке и он равен значению ф-ции в этой точке ,т.е. lim_xx0f(x) = f(x_o).

Это рав. Озн. Вып-е 3-х усл.: 1)f(x) определена в точке x₀ и в ее окрест. 2)f(x) имеет предел при xx₀ 3)предел ф-ции в точке x₀ равен знач. ф-ции в этой точке, т.е. вып. равенство lim_xx0f(x) = f(x_o). Т.к. lim_xx0x₀ = x₀, то lim_xx0f(x) = =f(lim_xx0x)= f(x₀). **Ф-ция y = f(x) наз. непрерывной в точке x₀, если она определена в точке x₀ и ее окрестности и вып. рав-во lim_x0y =0, т.е. беск. малому приращ. арг. соотв. беск. малое приращ. ф-ции.

#10 Непрерывность функции на отрезке: функция y=f(x) наз-ся непрерывной на [a,b] если она удовлетворяет определению непрерывности в каждой внутр точки этого отрезка внутри а также сущ lim(xa+0)f(x)=f(a) и lim(xb-0)f(x)=f(b)