20. Закон Джоуля-Ленца.

При прохождении по проводнику электрического тока проводник нагревается. Количесво выделяющегося тепла пропорционально сопротивлению квадрату силы тока и времени.

, если сила тока изменяется, то

Объяснение: рассмотрим проводник к которому приложено напряжение U. За время dt через каждое сечение проводника проходит заряд dq=idt. Это равносильно тому, что заряд переносится из одного конца проводника в дугой. При этом все силы поля совершают работу dA=Udq=Ui dt. Заменив U на Ri и проинтегрировав получаем:

dQ отнесённое к количеству времени называется мощностью тока 𝛚 = 𝛒j²= 𝛔E²

21.Природа носителей тока в металлах. Опыт Рикке и Стюарта-Толмена

Для выяснения природы носителей тока в металлах был поставлен ряд опытов. Опыт Рикке. В 1901 г. Рикке взял три цилиндра два медных и один алюминиевый с тщательно отшлифованными торцами. После взвешивания цилиндры были сложены вместе в последовательности медь - алюминий - медь. Через такой составной проводник непрерывно в течение года пропускался ток одного и того же направления. За все время через цилиндры прошел заряд, равный  . Взвешивание показало, что пропускание тока не оказало на массу цилиндров никакого влияния. При исследовании соприкасавшихся торцов под микроскопом не было обнаружено проникновение одного металла в другой.  Результаты опыта свидетельствовали о том, что перенос заряда в металлах осуществляется не атомами, а какими-то частицами, входящими в состав всех металлов. Чтобы отождествить носители тока в металлах с электронами, нужно было определить знак и числовое значение удельного заряда носителей. Если в металлах имеются способные перемещаться заряженные частицы, то при торможении металлического проводника эти частицы должны некоторое время продолжать двигаться по инерции, в результате чего в проводнике возникает импульс тока и будет перенесен некоторый заряд. Пусть проводник движется вначале со скоростью v (рис. 4.7).

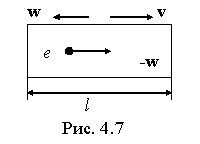
Начнем тормозить его с ускорением w. Продолжая двигаться по инерции, носители тока приобретают относительно проводника ускорение.  Такое же ускорение можно сообщить носителям в неподвижном проводнике, если создать в нем электрическое поле напряженностью  , т. е. приложить к концам проводника разность потенциалов 

.

где m и   - масса и заряд носителя; l - длина проводника. В этом случае по проводнику потечет ток силы  , где R - сопротивление проводника (Iсчитается положительным, если ток течет в направлении движения проводника). Следовательно, за время dt через каждое сечение проводника пройдет заряд

.

Заряд, прошедший за все время торможения, равен

.

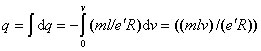(заряд положителен, если он переносится в направлении движения проводника). Таким образом, измерив l, v и R, а также заряд q, проходящий по цепи при торможении проводника, можно найти удельный заряд носителей. Направление импульса тока даст знак носителей. Количественный результат был получен Толменом и Стюартом в 1916 г. Катушка из провода длиной 500 м приводилась во вращение, при котором линейная скорость витков составляла  . Затем катушка резко тормозилась, и с помощью баллистического гальванометра измерялся заряд, протекавший в цепи за время торможения. Вычисленное значение удельного заряда носителей получалось очень близким к   для электронов. Таким образом, было экспериментально доказано, что носителями тока в металлах являются электроны. Существование в металлах свободных электронов можно объяснить тем, что при образовании кристаллической решетки от атомов металла отщепляются слабее всего связанные (валентные) электроны, которые становятся "коллективной" собственностью всего объема металла. Число атомов в единице объема равно , где   - плотность металла; М - масса моля;   - число Авогадро. Для металлов значения   заключены в пределах от   до  . Следовательно, для концентрации свободных электронов получаются значения порядка  .