- •1.Электрический заряд. Закон сохранения электрического заряда.. Электрическое поле.
- •2.Напряженность и потенциал электрического поля.
- •3.Электрический диполь
- •4.Циркуляция и ротор
- •5. Теорема Гаусса
- •6. Полярные и неполярные молекулы
- •7. Поверхностные и объёмные связанные заряды.
- •8. Вектор электрического смешения(d)
- •9. Условия на границе разделов двух диэлектриков
- •10. Сегнето электрики
- •11. Проводники в электрическом поле. Поле внутри проводника и у его поверхности. Распределение зарядов в проводнике.
- •12. Электроёмкость. Конденсаторы. Энергия заряженного конденсатора.
- •13. Объёмная плотность энергии электрического поля
- •14.Сила тока. Условия существования эл тока
- •15. Уравнение непрерывности
- •16. Электродвижущая сила
- •17. Закон Ома для однородного участка цепи. Сопротивление проводников.
- •18. Закон Ома для неоднородного участка цепи.
- •1 9. Разветвлённые цепи. Правила Кирхгофа.
- •20. Закон Джоуля-Ленца.
- •21.Природа носителей тока в металлах. Опыт Рикке и Стюарта-Толмена
- •22.Элементарная классическая теория металлов (теория Друде). Вывод законов Ома и Джоуля-Ленца в рамках теории Друде.
- •23.Закон Видемана-Франца. Затруднения классический теории металлов.
- •24.Работа выхода электронов из металла. Термоэлектронная эмиссия.
- •25.Ток в электролитах. Электролиз. Законы Фарадея для электролиза.
- •26.Ток в газах. Газовые разряды и их разновидности. Плазма.
- •27.Элементы зонной теории твердого тела.
- •28.Взаимодействие токов. Магнитное поле.
- •29.Закон Био-Савара-Лапласа.
- •30.Магнитное поле Бесконечно Длинного прямолинейного проводника с током. Магнитное поле кругового поля.
- •31.Теорема о циркуляции вектора магнитной индукции (закон полного тока)
- •32.Ампера закон
- •33. Контур с током
- •34.Работа, совершаемая при перемещении тока в магнитном поле.
- •39. Магнитные моменты атомов. Диа- и парамагнетизм.
- •40.Ферромагнетизм. Применение ферромагнетиков.
- •41. Явление электромагнитной индукции. Электродвижущая сила индукции.
- •42. Явление самоиндукции.
- •43. Ток при замыкании и размыкании цепи. Взаимная индукция.
- •44. Энергия магнитного поля
- •45. Вихревое электрическое поле.
- •46. Ток смешения.
- •47. Уравнение Максвелла.
- •48. Электромагнитная волна. Волновое уравнение.
- •49.Квазистационарный ток. Переменный ток
- •50. Переменный ток текущий через индуктивность
- •51. Переменный ток текущий через ёмкость
- •52. Цепь переменного тока содержащая индуктивность, ёмкость и активное сопротивление
- •53. Мощность выделяемая в цепи переменного тока
- •54. Генератор переменного тока
- •55. Электрический трансформатор. Передача электроэнергии на расстояние
- •56.Свободные колебания в колебательном контуре
- •57.Затухающие колебания в колебательном контуре
- •58. Вынужденные колебания в колебательном контуре
- •59.Излучение электромагнитных волн
42. Явление самоиндукции.
Электрический ток, текущий в замкнутом контуре, создает вокруг себя магнитное ноле, индукция которого, по закону Био —Савара—Лапласа, пропорциональна току. Сцепленный с контуром магнитный поток Ф поэтому пропорционален току в контуре:

где L — коэффициент пропорциональности, называемый индуктивностью контура.
При изменении силы тока в контуре будет изменяться также и сцепленный с ним магнитный поток; следовательно, в контуре будет индуцироваться ЭДС. Возникновение ЭДС индукции в проводящем контуре при изменении в нем силы тока называется самоиндукцией.
Из выражения (126.1) определяется единица индуктивности генри (Гн): 1 Гн — индуктивность такого контура, магнитный поток самоиндукции которого при токе в 1 А равен 1 Вб:
1 Гн = 1 Вб/А = 1 В • с/А.
Рассчитаем
индуктивность бесконечно длинного
соленоида. Тк полный магнитный поток
сквозь соленоид (потокосцепление)
равен . Подставив
это выражение в формулу (126.1), получим
. Подставив
это выражение в формулу (126.1), получим

т.
е. индуктивность соленоида зависит от
числа N
витков
соленоида, его длины l
площади
S
и
магнитной проницаемости
![]() вещества,
из которого изготовлен сердечник
соленоида.
вещества,
из которого изготовлен сердечник
соленоида.
Можно показать, что индуктивность контура в общем случае зависит только от геометрической формы контура, его размеров и магнитной проницаемости той среды, в которой он находится. В этом смысле индуктивность контура — аналог электрической емкости уединенного проводника, которая также зависит только от формы проводника, его размеров в диэлектрической проницаемости среды .
Применяя к явлению самоиндукции закон Фарадея получим ,что ЭДС самоиндукции
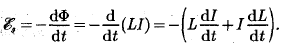
Если
контур не деформируется и магнитная
проницаемость среды не изменяется (в
дальнейшем будет показано, что последнее
условие выполняется не всегда),что
![]() и
и
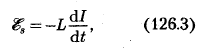
где знак «— » обусловлен правилом Ленца, согласно которому наличие индуктивности в контуре приводит к замедлению изменения тока в нем.
Если
ток со временем возрастает, то![]() т. е. ток самоиндукции
направлен
навстречу току, обусловленному внешним
источником, и замедляет его возрастание.
Если ток со временем убывает, то
т. е. ток самоиндукции
направлен
навстречу току, обусловленному внешним
источником, и замедляет его возрастание.
Если ток со временем убывает, то
![]() т. е. индукционный ток имеет такое же
направление, как и убывающий ток в
контуре, и замедляет его убывание. Таким
образом, контур, обладая определенной
индуктивностью, приобретает электрическую
инертность, заключающуюся в том, что
любое изменение тока тормозится тем
сильнее, чем больше индуктивность
контура.
т. е. индукционный ток имеет такое же
направление, как и убывающий ток в
контуре, и замедляет его убывание. Таким
образом, контур, обладая определенной
индуктивностью, приобретает электрическую
инертность, заключающуюся в том, что
любое изменение тока тормозится тем
сильнее, чем больше индуктивность
контура.
43. Ток при замыкании и размыкании цепи. Взаимная индукция.
При всяком изменении силы тока в проводящем контуре возникает ЭДС самоиндукции, в результате чего в контуре появляются дополнительные токи, называемые экстратоками самоиндукции.
Экстратоки самоиндукции, согласно правилу Ленца, всегда направлены так, чтобы препятствовать изменениям тока
в цепи, т.е. направлены противоположно току, создаваемому источником. При выключении источника тока экстратоки имеют такое же направление, что и ослабевающий ток. Следовательно, наличие индуктивности в цени приводит к замедлению исчезновения или установления тока в цепи.
Рассмотрим процесс выключения тока в цепи, содержащей источник тока с ЭДС резистор сопротивлением R и катушку индуктивностью L. Под действием внешней ЭДС в цепи течет постоянный ток
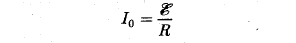
(внутренним сопротивлением источника тока пренебрегаем).
В
момент времени t
=
0 отключим источник тока. Ток в катушке
индуктивностью L
начнет
уменьшаться, что приведет к возникновению
ЭДС самоиндукции
![]() препятствующей, согласно правилу Ленца,
уменьшению тока.В каждый момент времени
ток в цепи определяется законом
препятствующей, согласно правилу Ленца,
уменьшению тока.В каждый момент времени
ток в цепи определяется законом
![]() или
или
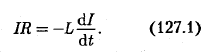
Разделив
в выражении (127.1) переменные, получим
![]() Интегрируя
это уравнение по I
(от I0
до I)
и t(от
0 до t),
находим
Интегрируя
это уравнение по I
(от I0
до I)
и t(от
0 до t),
находим
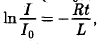 или
или
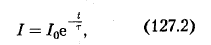
где
![]() — постоянная, называемая временем
релаксации.
— постоянная, называемая временем
релаксации.
Из (127.2) следует, что т есть время, в течение которого сила тока уменьшается в е раз.
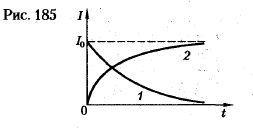
Таким образом, в процессе отключения источника тока сила тока убывает по экспоненциальному закону (127.2) и определяется кривой 1 на рис. 185. Чем больше индуктивность цепи и меньше ее сопротивление, тем больше T и, следовательно, тем медленнее уменьшается ток в цепи при ее размыкании.
При
замыкании цепи помимо внешней ЭДС
возникает ЭДС самоиндукции
![]() ,
препятствующая, согласно правилу
,
препятствующая, согласно правилу
Ленца,
возрастанию тока. По закону Ома,
![]() или
или
![]()
Введя
новую переменную
![]() преобразуем
это уравнение к виду
преобразуем
это уравнение к виду
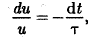
где т — время релаксации.
В
момент замыкания (t
=
0) сила тока I=
0 и u
=-ε. Следовательно, интегрируя по u
(от — ε до IR-
ε)и
t
(от
0 до t),
находим
![]() или
или
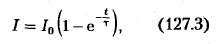
где
![]() — установившийся ток (при
t
—>
оо).
— установившийся ток (при
t
—>
оо).
Таким образом, в процессе включения источника тока нарастание силы тока в цепи задается функцией (127.3) и определяется кривой 2 на рис. 185.
Взаимная индукция.
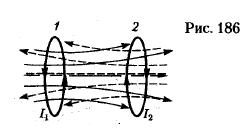
Рассмотрим два неподвижных контура (1 и 2), расположенных достаточно близко друг от друга (рис. 186). Если в контуре 1 течет ток IХ, то магнитный поток, создаваемый этим током (поле, создающее этот поток, на рисунке изображено сплошными линиями), пропорционален Iх. Обозначим через Ф21 часть потока, которая пронизывает контур 2. Тогда
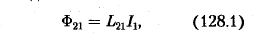
где L21 — коэффициент пропорциональности.
Если ток IХ изменяется, то в контуре 2 индуцируется ЭДС которая по закону Фарадея равна и противоположна по знаку скорости изменения магнитного потока Ф21, созданного током в первом кoнтуре и пронизывающего второй:
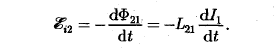
Явление возникновения ЭДС в одном из контуров при изменении силы тока в другом называется взаимной ин дукцией. Коэффициенты пропорциональности L21 и L12 называются взаимной индуктивностью контуров. Расчеты, подтверждаемые опытом, показывают, что
![]()
Коэффициенты L21 и L12 зависят от геометрической формы, размеров, взаимного расположения контуров и от магнитной проницаемости окружающей контуры среды. Единица взаимной индуктивности та же, что и для индуктивности, — генри (Гн).