1

2

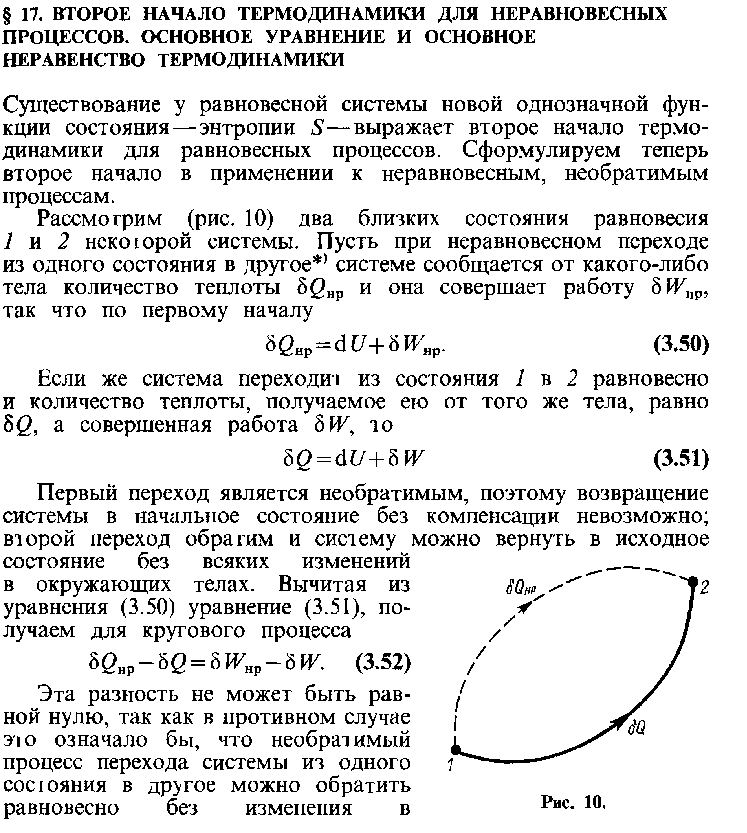
3

4

5

6

7

8

9

10

11

12

13

14

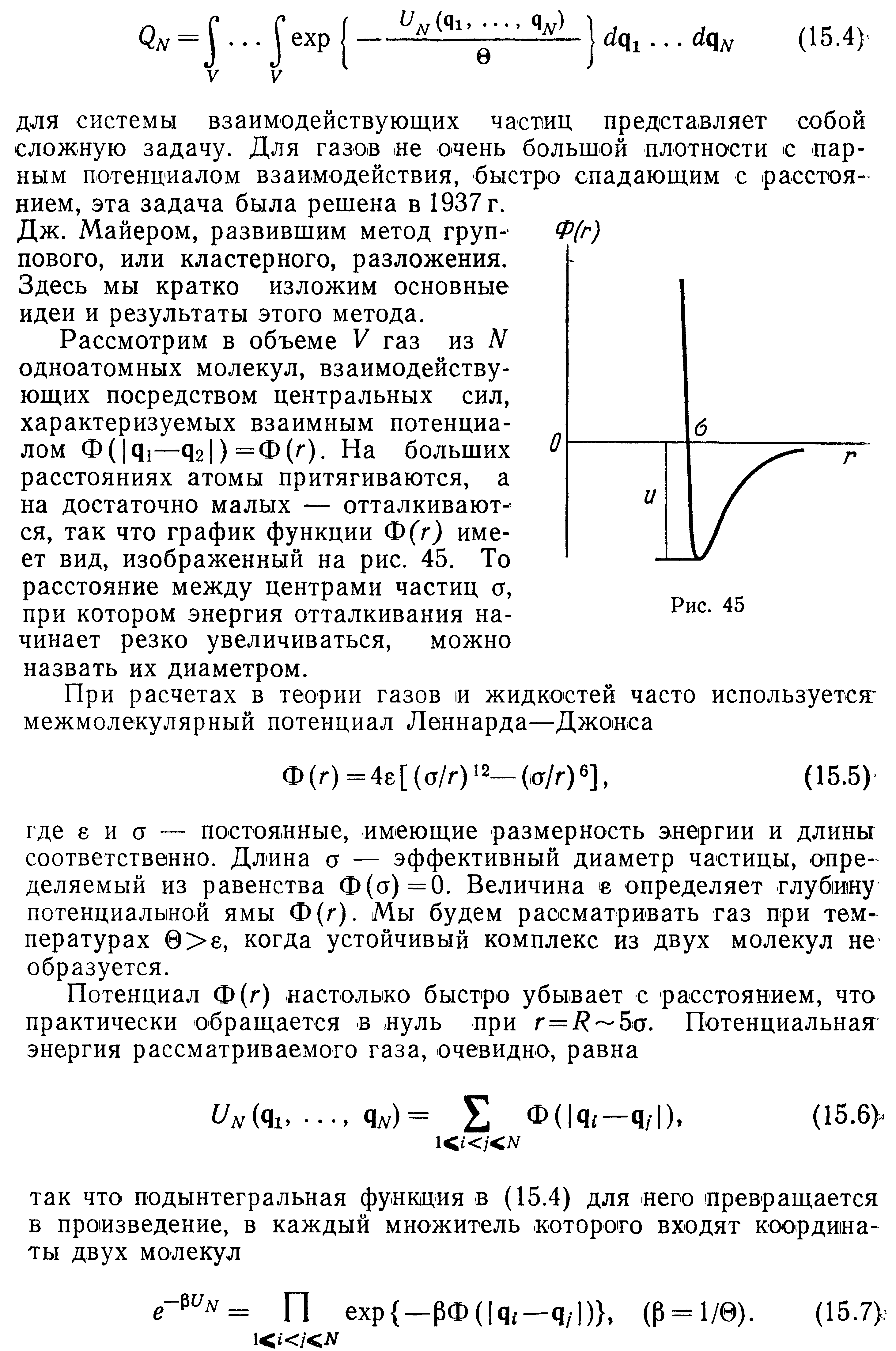
15

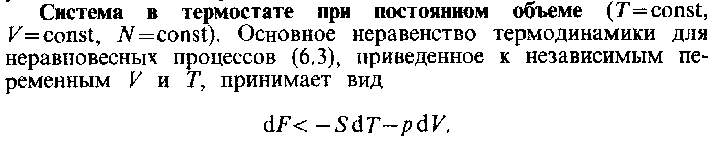
16

17

18

19

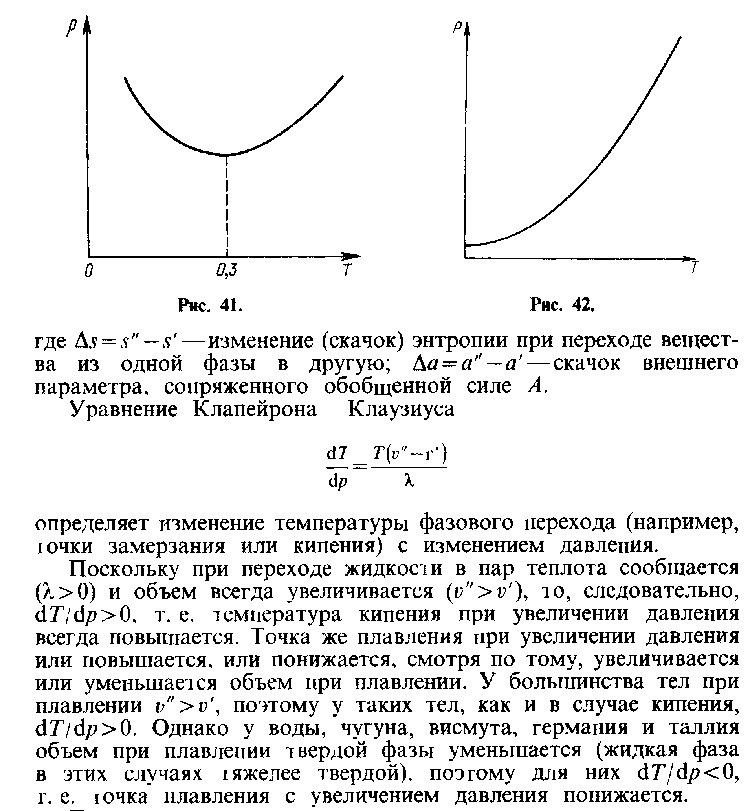
20

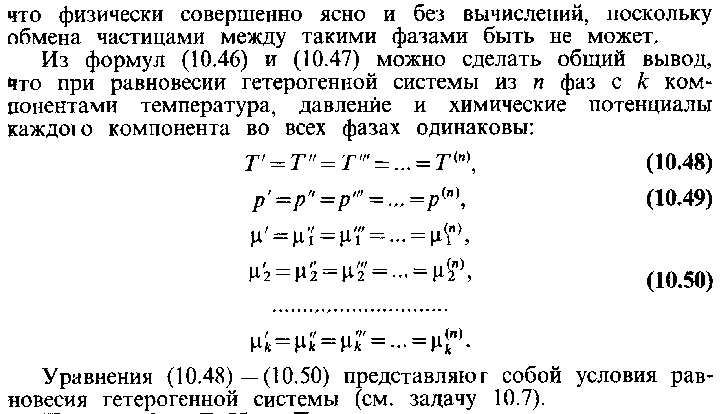
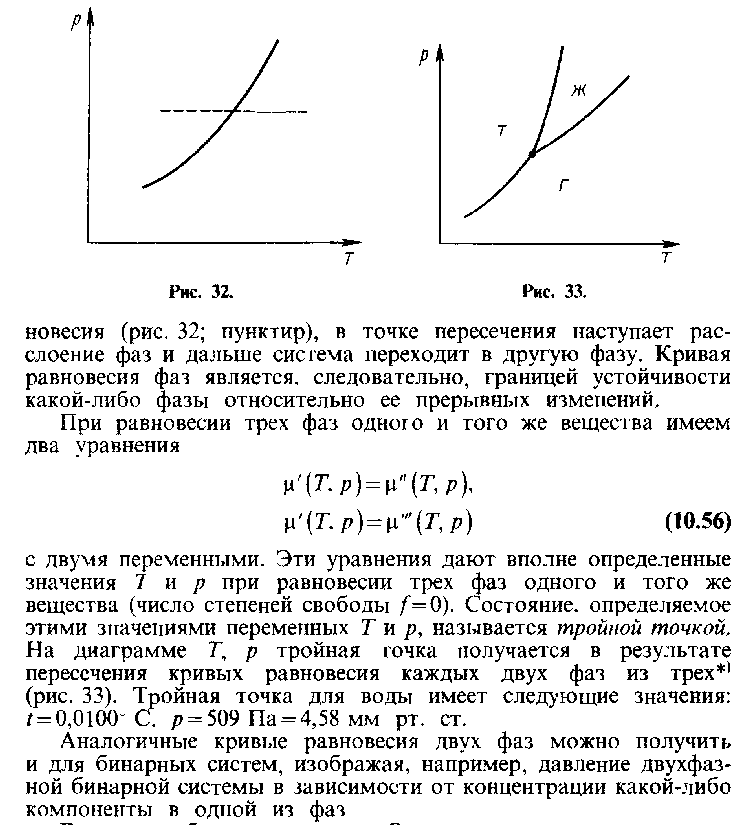
21

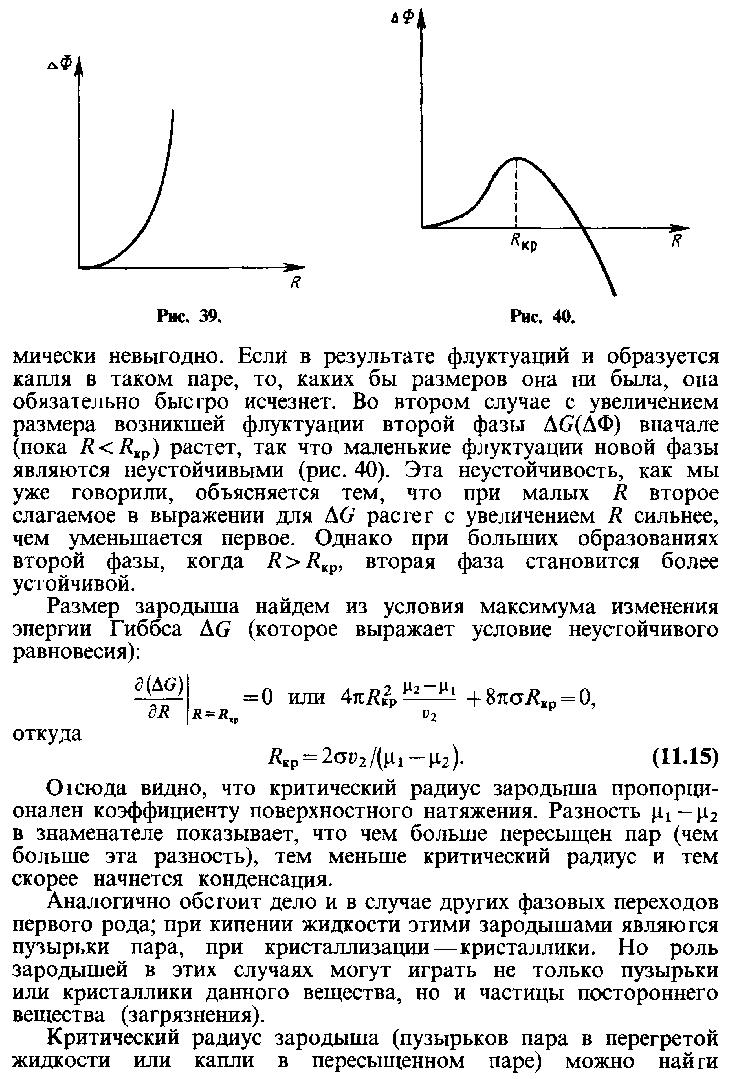
22

23

Теоре́ма Лиуви́лля, названная по имени французского математика Жозефа Лиувилля, является ключевой теоремой в математической физике, статистической физике и гамильтоновой механике. Теорема Лиувилля гласит

Функция распределения гамильтоновой системы постоянна вдоль любой траектории в фазовом пространстве.

Теорема утверждает сохранение во времени фазового объема, или плотности вероятности в фазовом пространстве.

Уравнение Лиувилля

Уравнение Лиувилля описывает эволюцию во времени функции распределения (плотности вероятности) гамильтоновой системы в  -мерном фазовом пространстве (  — количество частиц в системе). Рассмотрим гамильтонову систему с координатами   и сопряжёнными импульсами  , где  ,  . Тогда распределение в фазовом пространстве   определяет вероятность   того, что система будет находиться в элементе объёма   своего фазового пространства.

Уравнение Лиувилля описывает эволюцию   во времени   согласно правилу нахождения полной производной функции с учётом несжимаемости потока в фазовом пространстве:

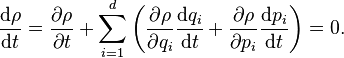
Производные фазовых координат по времени для гамильтоновых систем описываются согласно уравнениям Гамильтона:

Простое доказательство теоремы состоит в наблюдении, что эволюция   определяется уравнением неразрывности (непрерывности):

где   — скорость перемещения исследуемого объёма фазового пространства:

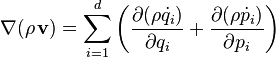
и замечанием, что разность между этим выражением и уравнением Лиувилля определяется только слагаемым описывающим дивергенцию, а именно её отсутствие, что означает отсутствие источников или стоков плотности вероятности:

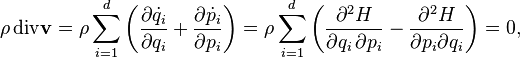
где   — гамильтониан, и были использованы уравнения Гамильтона. Это можно представить как движение через фазовое пространство «потока жидкости» точек системы. Теорема означает, что производная Лагранжа илисубстанциональная производная плотности   равна нулю. Это следует из уравнения непрерывности, так как поле скоростей   в фазовом пространстве бездивергентно, что в свою очередь вытекает из гамильтоновых уравнений для консервативных систем.

Запись через скобку Пуассона

Используя скобку Пуассона, имеющее в канонических координатах   вид

уравнение Лиувилля для гамильтоновых систем приобретает вид

Запись с использованием оператора Лиувилля

При помощи оператора Лиувилля

для гамильтоновых систем уравнение приобретает вид

24

25

26

Статистический смысл энтропии. Энтропия идеального газа. Флуктуации.

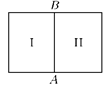
Рассмотрим закрытый сосуд, разделенный перегородкой , на две одинаковые части и . Пусть в части сосуда находится молекул идеального газа, а в части – ни одной. В момент времени мгновенно удалим перегородку. Молекулы из части начнут переходить в часть . В какой-то момент времени количества молекул в первой и второй частях примерно выровняются. Так же выровняются потоки туда и обратно. Мы будем наблюдать динамическое равновесие, а не статистическое.

Статистическое равновесие предполагает, что , а в нашем случае это правила почти никогда не соблюдается. Для такой системы нужно оперировать не мгновенными значениями и , а их средними значениями, взятыми за достаточно длительный промежуток времени: . Самопроизвольные отклонения чисел и , а так же любых других физических величин от их средних значений, обусловленные тепловым движением, называются флуктуациями.

Рассмотрим сосуд всего с одной молекулой идеального газа. Она равновероятно может попасть в часть сосуда или . Вероятность такого попадания . Введем в сосуд вторую молекулу. Молекулы идеального газа не взаимодействуют между собой и их попадания в ту или иную часть сосуда – события независимые. Вероятность того, что они обе окажутся в части сосуда (по теореме умножения вероятностей): . Если в сосуде молекул, то вероятность их общего попадания в часть будет . Если полный объем сосуда , то вероятность попадания отдельной молекулы идеального газа в некоторый объем , выделенный из общего объема, равна . Вероятность того, что в окажутся молекул, равна

  .

Предположим, что между энтропией и вероятностью есть связь, выражающаяся формулой , где – одна и та же для всех тел. Рассмотрим две независимые подсистемы в состояниях с вероятностями и . Энтропии этих состояний – и . Объединим подсистемы в систему и обозначим вероятность ее состояния через , а энтропию через . Т.к. подсистемы независимы, то , значит . Учтем, что энтропия сложной системы должна быть равна сумме энтропий составляющих ее независимых подсистем

. Из этого следует, что . Предположим, что переменные и изменяются так, что , тогда . Продифференцируем оба выражения и получим: , при условии . После почленного деления –

.

Т.к. в левой и правой частях разные , то можно сделать вывод, что функция

 

не изменяется при изменении аргумента. Это значит она является некой универсальной постоянной (обозначим ее через ), одной и той же для всех тел.

  .

Подставим последнее соотношение в уравнение и получим

  ,

откуда .

      Значит – уравнение Больцмана.

Пусть и – объемы моля газа в начальном и конечном состоянии при одной и той же температуре. Отношения вероятностей найдем по формуле , поочередно предположив: , . Далее найдем разность энтропий

  .

Из определения энтропии известно, что если теплоемкость не зависит от температуры, то

  ,

тогда .

Сравнивая два уравнения для , получим – постоянная Больцмана.

27

28

29

30

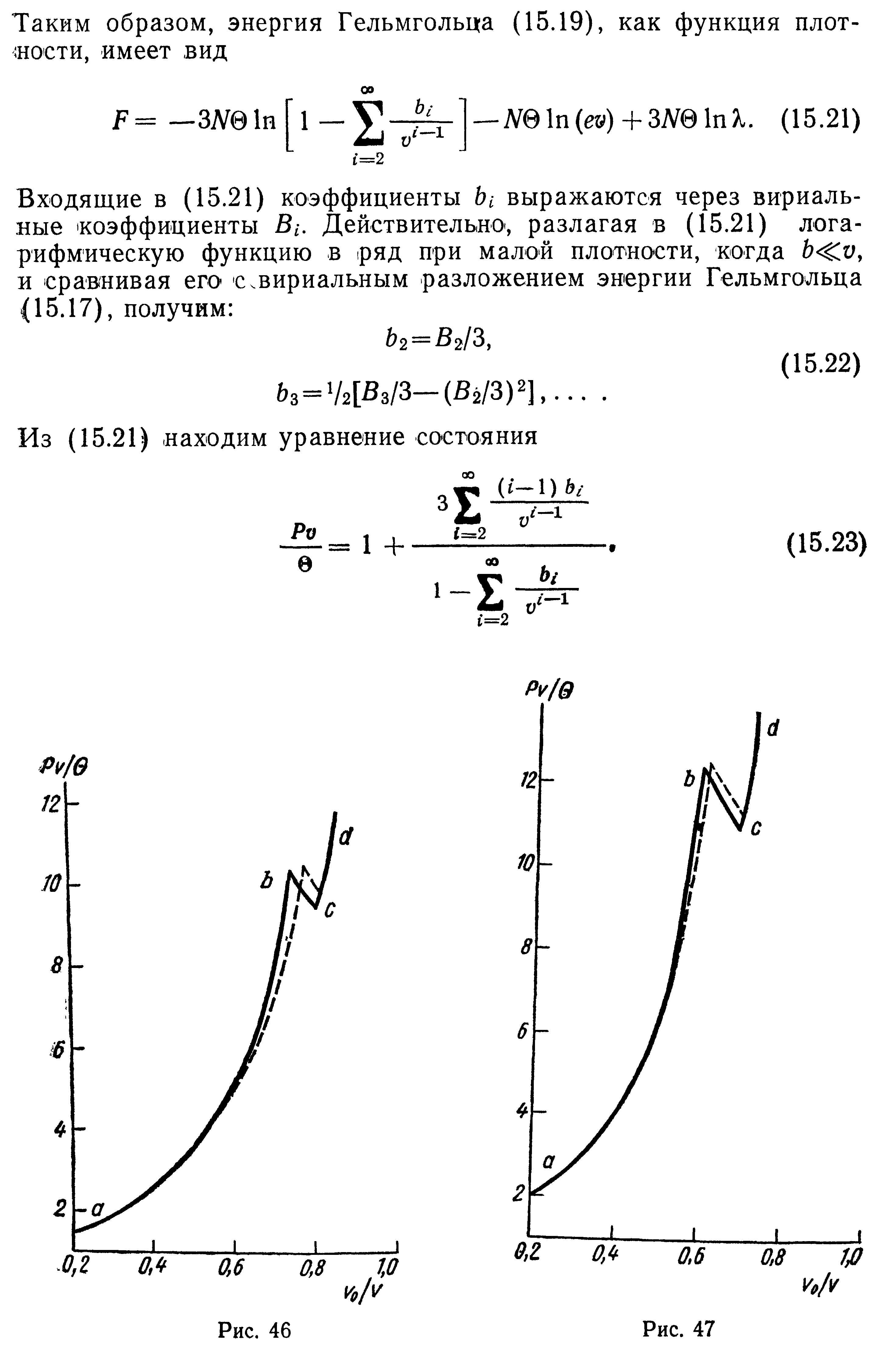
31

32,33