16. Сформулювати локальну теорему Муавра-Лапласа.

Якщо ймовірність появи випадкової події в кожному з n незалеж­них експериментів є величиною сталою і дорівнює , то для великих значень n і m імовірність того, що випадкова подія А настане m раз, подається такою асимптотичною формулою: ,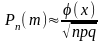

де 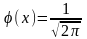^℮ називається функцією Гаусса. Функція Гаусса протабульована, де .

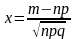17. Сформулювати інтегральну теорему Муавра-Лапласа.

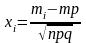Якщо ймовірність появи випадкової події в кожному з n незалеж­них експериментів є величиною сталою і дорівнює , то для великих значень n імовірність появи випадкової події від m_і до m_j раз обчислюється за такою асимптотичною формулою: , де , а 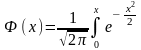є функцією Лапласа.

18. Функція Гаусса та її властивості.

^℮ називається функцією Гаусса.

Функція Гаусса протабульована, де .

Властивості функції Гаусса:

1) 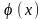визначена на всій осі абсцис; ; 2) є функцією парною: ;

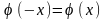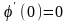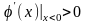3) ; 4) ; ; ; ; отже, 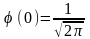— максимум функції Гаусса; 5) .

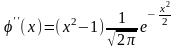
Таким чином, х₁ = –1, х₂ = 1 будуть точками перегину. При цьому

; ; .

19. Функція Лапласа та її властивості.

є функцією Лапласа

Властивості функції Лапласа:

1. Ф(x) визначена на всій осі абсцис. 2. Ф(–x) = – Ф(x), отже, Ф(x) є непарною функцією.

3. Ф(0) = 0. 4. 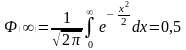 , оскільки 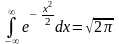є інтегралом Пуассона.

5. Ф(–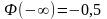 , як непарна функція. 6.  , отже, Ф (х) є функцією неспадною.

7. Ф"(0) = 0; Таким чином, x = 0 є точкою перегину.

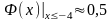
20. Формула Пуассона, умови її використання.

Точність асимптотичних формул для великих значень n — числа повторних незалежних експериментів за схемою Бернуллі — знижується з наближенням p до нуля. Тому при 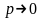за умови np = a = const імовірність появи випадкової події m раз обчислюється за такою асимптотичною формулою: , яка називається формулою Пуассона.

n велике, а р мале число – використовується для масових малоймовірних випадкових подій.

21. Означення випадкової величини, дискретної та неперервної випадкових величин.

Розглянемо такий простір елементарних подій, в якому кожній елементарній події Ώ відповідає одне і лише одне число х або набір чисел 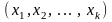, тобто на множині Ώ визначена певна функ­ція , яка кожній елементарній події ставить у відповідність певний елемент одновимірного простору R₁ або n-вимірного простору R_n. Цю функцію називають випадковою величиною.

Отже, величина називається випадковою, якщо внаслідок проведення експерименту під впливом випадкових факторів вона набуває того чи іншого можливого числового значення з певною ймовірністю.

Якщо існує скінчена або злічена множена значень, то таку величину називають дискретною. Якщо кількість можливих значень є нескінченною і задати її за допомогою ряду розподілу неможливо, то величина неперервна.