86) Ймовірність переходу за n кроків.

Нехай маємо однорідний ланцюг Маркова з матрицею ймовірностей переходу P. Позначимо:

Оскільки ланцюг Маркова є однорідним то дане означення не залежить від n. Тоді виконується рівність

де    — елемент i-го рядка і j-го стовпчика матриці P^k.

87) Замкнуті множини станів.

За́мкнута множина́ — підмножина простору доповнення до якої відкрита.

Означення

Нехай дано топологічний простір . Множина   називаєтся замкнутою відносно топології  , якщо існує відкрита множина   така що 

Властивості

Із аксіом означення топології випливає:

• перетин будь-якого набору замкнутих множин є замкнутою множиною

• об'єднання скінченної кількості замкнутих множин є замкнутою множиною

88) Класифікація станів. Неповоротний стан.

Класифікація станів:

1. Ергодичний стан

Нехай задано простір станів марковського процесу і певну під­множину станів 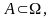при цьому буде доповненням до А.

Якщо з кожного стану підмножини А можна перейти до будь-якого стану і при цьому до стану процес не зможе перейти ні з одного зі станів, які належать підмножині А, то в цьому разі А називають ергодичною множиною, або множиною ергодичного стану процесу. Одного разу потрапивши до ергодичної множини, процес ніколи не зможе залишити її, і з цього моменту часу переміщуватиметься лише серед тих станів, які належать ергодичній множині А.

Отже, ергодичний стан є елементом ергодичної множини.

2. Нестійкі стани

Нехай задано простір станів випадкового процесу 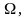а також 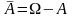. Тоді, якщо будь-який стан підмножини А може бути досягнений із будь-якого іншого стану цієї самої під- множини і при цьому існує хоча б один стан , із якого процес може перейти до стану 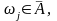то підмножину станів А називають нестійкою.

Нестійкий стан є елементом нестійкої множини А.

3. Поглинальні стани

Якщо ергодична множина має лише один стан, то його називають поглинальним. Одного разу потрапивши до цього стану, процес у ньому залишається назавжди.

У загальному випадку марковський процес може мати одну, дві і більше ергодичних множин, але при цьому не мати нестійких множин.

89) Ергодична властивість неперіодичних ланцюгів. Стаціонарний розподіл.

Ергоди́чність — спеціальна властивість деяких (динамічних) систем, яка полягає в тому, що в процесі еволюції такої системи майже кожна точка її з певною ймовірністю проходить поблизу будь-якої іншої точки системи. Тоді при розрахунках час, який важко розраховувати, можна замінити фазовими (просторовими) показниками. Система, в якій фазові середні збігаються з часовими, називається ергодичною.

Перевага ергодичних динамічних систем полягає в тому, що при достатньому часу спостереження такі системи можна описувати статистичними методами. Наприклад, температура газу — це міра середньої енергії молекули, ринкова ціна компанії — це міра похідних функцій від даних бухгалтерської звітності. Звісно, необхідно попередньо довести ергодичність даної системи.

Для ергодичних систем математичне сподівання по часових рядах має збігатися з математичним сподіванням по просторових рядах.

Для однорідного ланцюга Маркова вектор   називається стаціонарним розподілом, якщо сума його елементів   дорівнює 1 і виконується рівність

Нерозкладний ланцюг має стаціонарний розподіл тоді й лише тоді, коли всі його стани є позитивно рекурентними. В цьому випадку вектор   є єдиним і виконується рівність: