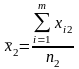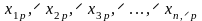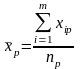- •Означення та приклади подій: випадкова, достовірна, неможлива, елементарна, складна.
- •Означення та приклад повної групи подій та простору елементарних подій.
- •Класичне означення ймовірності випадкової події.
- •Сформулювати аксіоми класичної теорії ймовірностей.
- •Дати означення та вказати властивості перестановки, сполучення, комбінації елементів.
- •Дати означення відносної частоти появи події.
- •Дати геометричне та статистичне означення ймовірності.
- •Дати визначення умовної ймовірності.
- •Формула множення ймовірностей для залежних та незалежних подій.
- •Формула для обчислення появи хоча б однієї події .
- •Формула повної ймовірності.
- •Формули Байєса.
- •Означення експерименту за схемою Бернуллі.
- •Формула Бернуллі для обчислення ймовірностей, умова використання. Наслідки.
- •Найімовірніше число появ події в схемі Бернуллі.
- •Сформулювати локальну теорему Муавра-Лапласа.
- •Властивості функції Лапласа:
- •Означення випадкової величини, дискретної та неперервної випадкових величин.
- •Закон розподілу випадкової величини.
- •Інтегральна функція розподілу випадкової величини: означення. Властивості.
- •Диференціальна функція розподілу (щільність розподілу) випадкової величини: означення. Властивості.
- •Математичне сподівання випадкової величини: означення, властивості.
- •Дисперсія та середньоквадратичне відхилення випадкової величини: означення, властивості.
- •Властивості дисперсії
- •Мода, медіана випадкової величини.
- •Початкові та центральні моменти.
- •Асиметрія, ексцес.
- •Означення багатовимірної випадкової величини.
- •Означення закону розподілу багатовимірної випадкової величини.
- •Основні числові характеристики для системи двох дискретних випадкових величин.
- •Коефіцієнт кореляції та його властивості.
- •Функція розподілу ймовірностей та щільність ймовірностей системи
- •Двовимірний нормальний закон розподілу.
- •Закон розподілу Бернулі
- •Біноміальний закон розподілу двв. Числові характеристики.
- •Пуасонівський закон розподілу двв, числові характеристики.
- •Геометричний закон розподілу двв, числові характеристики.
- •Гіпергеометричний закон розподілу двв, числові характеристики.
- •Рівномірний закон розподілу нвв.
- •Нормальний закон розподілу.
- •Показниковий закон та його використання в теорії надійності та теорії черг.
- •Розподіл
- •Розподіл Стьюдента. Розподіл Фішера. (45-46)
- •Правило трьох сигм. Логарифмічний нормальний закон.
- •Функції одного дискретного випадкового аргументу.
- •.Числові характеристики функції одного дискретного випадкового аргументу.
- •Функції неперервного випадкового аргументу та їх числові характеристики.
- •Функції двох випадкових аргументів та їх числові характеристики.
- •Числові характеристики функції дискретного випадкового аргументу
- •Нерівності Чебишева та їх значення.
- •Теорема Чебишева.
- •Теорема Бернуллі.
- •Центральна гранична теорема теорії ймовірностей ( теорема Ляпунова) та її використання у математичній статистиці.
- •Предмет і задачі математичної статистики.
- •Утворення вибірки. Генеральна та вибіркова сукупність.
- •Статистичні розподіли вибірок.
- •Емпірична функція розподілу, гістограма та полігон.
- •Числові характеристики: вибіркова середня, дисперсія вибірки, середньоквадратичне відхилення.
- •Мода й медіана, емпіричні початкові та центральні моменти, асиметрія та ексцес.
- •Дати визначення статистичної оцінки.
- •Точкові та інтервальні статистичні оцінки.
- •Дати визначення довірчого інтервалу.
- •Що таке нульова та альтернативна статистичні гіпотези.
- •Перевірка (правдивості нульової) гіпотези про нормальний закон розподілу ознаки генеральної сукупності.
- •Емпіричні та теоретичні частоти.
- •Критерії узгодження Пірсона та Колмогорова.
- •Помилки першого та другого роду.
- •Статистичний критерій. Критична область.
- •Дати означення моделі експерименту.
- •Дати поняття одно факторний аналіз.
- •Загальна дисперсія, між групова та внутрішньогрупова дисперсії.
- •. Поняття про функціональну, статистичну та кореляційну залежності.
- •Рівняння лінійної регресії. Довірчий інтервал для лінії регресії
- •Вибірковий коефіцієнт кореляції.
- •Множинна регресія, множинний коефіцієнт кореляції та його властивості.
- •Нелінійна регресія.
- •85) Визначення та приклади ланцюгів Маркова.
- •Інтуїтивне визначення
- •Формальне визначення
- •Граф переходів ланцюга Маркова
- •86) Ймовірність переходу за n кроків.
- •87) Замкнуті множини станів.
- •88) Класифікація станів. Неповоротний стан.
- •1. Ергодичний стан
- •2. Нестійкі стани
- •3. Поглинальні стани
- •89) Ергодична властивість неперіодичних ланцюгів. Стаціонарний розподіл.
- •90) Періодичні ланцюги.
- •91) Загальний марковський процес (Ланцюг Маркова з неперервним часом).
- •92) Гранична поведінка перехідних ймовірностей ланцюга Маркова.
- •93) Гілчастий процес.
- •94) Алгебраїчний підхід вивчення скінченних ланцюгів Маркова.
- •96) Випадковий проце, стаціонарний у широкому сенсі.
- •97) Аналіз кореляційної функції. Ергодичність.
- •100) Рівняння Колмогорова - Чепмена
Статистичний критерій. Критична область.
Для
перевірки правильності висунутої
статистичної гіпотези вибирають так
званий статистичний критерій, керуючись
яким відхиляють або не відхиляють
нульову гіпотезу. Статистичний критерій,
котрий умовно позначають через K,
є випадковою величиною, закон розподілу
ймовірностей якої нам заздалегідь
відомий. Так, наприклад, для перевірки
правильності
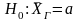 як статистичний критерій K
можна взяти випадкову величину, яку
позначають через K = Z,
що дорівнює
як статистичний критерій K
можна взяти випадкову величину, яку
позначають через K = Z,
що дорівнює
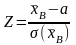 і яка має нормований нормальний закон
розподілу ймовірностей. При
великих обсягах вибірки (n > 30)
закони розподілу статистичних
критеріїв наближатимуться до нормального.
Спостережуване значення критерію, який
позначають через K,
обчислюють за результатом вибірки.
і яка має нормований нормальний закон
розподілу ймовірностей. При
великих обсягах вибірки (n > 30)
закони розподілу статистичних
критеріїв наближатимуться до нормального.
Спостережуване значення критерію, який
позначають через K,
обчислюють за результатом вибірки.
Множину
всіх можливих значень статистичного
критерію K
можна поділити на дві підмножини А
і
 ,
які не перетинаються.
,
які не перетинаються. .
Сукупність значень статистичного
критерію K
А,
за яких нульова гіпотеза не відхиляється,
називають областю
прийняття нульової гіпотези.
Сукупність
значень статистичного критерію K
,
за яких нульова гіпотеза не приймається,
називають критичною
областю.
Отже,
А
— область прийняття Н0,
— критична область, де Н0
відхиляється. Точку або кілька точок,
що поділяють множину
на підмножини А
і
,
називають критичними
і позначають через Kкр.
Існують три види критичних областей:
Якщо при K < Kкр
нульова
гіпотеза відхиляється, то в цьому разі
ми маємо лівобічну критичну область,
яку умовно можна зобразити (рис. 1).
.
Сукупність значень статистичного
критерію K
А,
за яких нульова гіпотеза не відхиляється,
називають областю
прийняття нульової гіпотези.
Сукупність
значень статистичного критерію K
,
за яких нульова гіпотеза не приймається,
називають критичною
областю.
Отже,
А
— область прийняття Н0,
— критична область, де Н0
відхиляється. Точку або кілька точок,
що поділяють множину
на підмножини А
і
,
називають критичними
і позначають через Kкр.
Існують три види критичних областей:
Якщо при K < Kкр
нульова
гіпотеза відхиляється, то в цьому разі
ми маємо лівобічну критичну область,
яку умовно можна зобразити (рис. 1).

Якщо
при
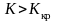 нульова гіпотеза відхиляється, то в
цьому разі маємо правобічну критичну
область
нульова гіпотеза відхиляється, то в
цьому разі маємо правобічну критичну
область

Якщо
ж при
 і при
і при
 нульова гіпотеза відхиляється, то маємо
двобічну критичну область
нульова гіпотеза відхиляється, то маємо
двобічну критичну область

Лівобічна і правобічна області визначаються однією критичною точкою, двобічна критична область — двома критичними точками, симетричними відносно нуля.
Дати означення моделі експерименту.
Випадковий експеримент (випадкове випробування, випадковий досвід) - математична модель відповідного реального експерименту, результат якого неможливо точно передбачити. Математична модель повинна задовольняти вимогам: вона повинна бути адекватна і адекватно описувати експеримент; повинна бути визначена сукупність безлічі спостережуваних результатів в рамках розглянутої математичної моделі при строго певних фіксованих початкових даних, що описуються в рамках математичної моделі; повинна існувати принципова можливість здійснення експерименту з випадковим результатом наскільки угодне кількість разів при незмінних вхідних даних, (де - кількість вироблених експериментів); повинно бути доведено вимогу або апріорі прийнята гіпотеза про стохастичною стійкості відносної частоти для будь-якого спостережуваного результату, визначеного в рамках математичної моделі.
Дати поняття одно факторний аналіз.
Дисперсійний аналіз дає загальну схему перевірки статистичних гіпотез, що базуються на вивченні різних джерел варіації або неоднорідності. Однофакторний дисперсійний аналіз використовується для перевірки значимих відмінностей між середніми значеннями вибірок, що розглядаються. Дані аналізу – це k незалежних одновимірних вибірок, елементи яких вимірюються в однакових одиницях. Кількість елементів кожної вибірки може бути різною. Однофакторний аналіз порівнює 2 джерела варіації: - міжгрупова (між вибірками), -внутрішньогрупова (в середині однієї вибірки).
Нехай потрібно дослідити вплив на ознаку Х певного одного фактора. Результати експерименту ділять на певне число груп, які відрізняються між собою ступенем дії фактора.
Для зручності в проведенні необхідних обчислень результати експерименту зводять в спеціальну таблицю:
Ступінь впливу фактора (групи) |
Спостережуване значення ознаки Х |
Групові середні |
Загальна середня |
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
…. |
… |
… |
|
р |
|
|


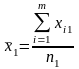
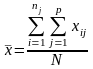 ,
,