61. Утворення вибірки. Генеральна та вибіркова сукупність.

Нехай потрібно вивчити сукупність об’єктів відносно деякої якісної або кількісної ознаки, які характеризують ці об’єкти. Розглядаючи одну ознаку припускають, що інші ознаки рівноправні або множина об’єктів однорідна, такі множини однорідних об’єктів назив статистичною сукупністю.

Наприклад: якщо дослідити партію деталей якісною ознакою, буде: стандартність або нестандартність кожної деталі; кількісною ознакою – розмір деталі. Кількісні ознаки можуть бути дискретними або неперервними.

Перевірку сукупності деталей можна провести 2 способами:

• Провести перевірку всіх деталей

• Перевірити лише певну частину деталей

Вибірковою сукупністю (вибіркою) назив. сукупність випадково взятих об’єктів.

Генеральною сукупністю назив сукупність об’єктів з яких зроблено вибірку.

Об’ємом сукупності (вибіркової або генеральної) назив кількість об’єктів цієї сукупності.

Вибірки можуть бути повторні та безповторні. Повторною назив вибірка, при якій відібраний об’єкт повертається до генеральної сукупності. Безповторна – коли об’єкт не повертається до генеральної сукупності.

Репрезентативна вибірка – представницька, коли її здійснюють випадково. Кожен об’єкт вибірки відібраний випадок з генеральної сукупності, якщо всі її об’єкти мають однакову ймовірність потрапити до вибірки.

62. Статистичні розподіли вибірок.

Для детального вивчення вибірки в простому статистичному ряді доцільно зробити обробку, згрупувати члени вибіркової сукупності, що приймають рівні значення, ознаки або значення в деякому інтервалі.

Нехай з генеральної сукупності взята вибірка об’єктів для вивчення ознаки Х, яка приймає значення х₁ – n₁ раз … х_m – m раз. Значення х₁… х_m - варіанти ознаки х. варіанти, що записані до таблиці у зростаючому порядку назив варіаційним рядом.

Кількість спостережень – n₁ , n₂ …n_m - назив рядом частот. Сума усіх частот назив об’ємом вибірки, обчислюється за формулою

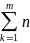
Відношення частоти m_k до об’єму вибірки n_k назив відносною частотою варіант х_k. Сума всіх відносних частот вибірки = 1

– відносна частота варіант х_k . Статистичним розподілом вибірки назив перелік варіант та відповідних їм частот або відносних частот.

63. Емпірична функція розподілу, гістограма та полігон.

Емпірична функція розподілу або функція розподілу вибірки назив 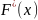, яка визначає для кожного значення х відносну частоту події і за аналогією Х<х

Інтегральна функція розподілу F(x) генеральної сукупності назив теоретичною функцією розподілу, вона відрізняється від емпіричної тим, що визначає ймовірність події Х<х, а емпірична відносну частоту цієї події.

Властивості:

1. 0< <1

2. Зростаюча.

3. =

Полігоном частот називається ламана, відрізки якої з’єднують точки (x₁;n₁)(x₂;n₂)…(x_m; n_m) ; відносних частот (x₁; w₁) (x₂; w₂)…(x_m; w_m).

Гістограмою частот назив східчасту фігуру, яка складається з прямокутників основами яких є відрізки довжиною x_k-x_k-1, а висоти .

Гістограмою відносних частот назив східчасту фігуру, яка складається з прямокутників основами яких є відрізки довжиною x_k-x_k-1, а висоти - щільність частоти.

Площа гістограми частот = об’єму вибірки, а площа гістограми відносних частот = 1.

Гістограма – наближений графік диференціальної функції розподілу.