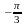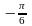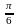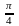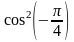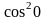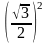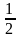- •Означення та приклади подій: випадкова, достовірна, неможлива, елементарна, складна.
- •Означення та приклад повної групи подій та простору елементарних подій.
- •Класичне означення ймовірності випадкової події.
- •Сформулювати аксіоми класичної теорії ймовірностей.
- •Дати означення та вказати властивості перестановки, сполучення, комбінації елементів.
- •Дати означення відносної частоти появи події.
- •Дати геометричне та статистичне означення ймовірності.
- •Дати визначення умовної ймовірності.
- •Формула множення ймовірностей для залежних та незалежних подій.
- •Формула для обчислення появи хоча б однієї події .
- •Формула повної ймовірності.
- •Формули Байєса.
- •Означення експерименту за схемою Бернуллі.
- •Формула Бернуллі для обчислення ймовірностей, умова використання. Наслідки.
- •Найімовірніше число появ події в схемі Бернуллі.
- •Сформулювати локальну теорему Муавра-Лапласа.
- •Властивості функції Лапласа:
- •Означення випадкової величини, дискретної та неперервної випадкових величин.
- •Закон розподілу випадкової величини.
- •Інтегральна функція розподілу випадкової величини: означення. Властивості.
- •Диференціальна функція розподілу (щільність розподілу) випадкової величини: означення. Властивості.
- •Математичне сподівання випадкової величини: означення, властивості.
- •Дисперсія та середньоквадратичне відхилення випадкової величини: означення, властивості.
- •Властивості дисперсії
- •Мода, медіана випадкової величини.
- •Початкові та центральні моменти.
- •Асиметрія, ексцес.
- •Означення багатовимірної випадкової величини.
- •Означення закону розподілу багатовимірної випадкової величини.
- •Основні числові характеристики для системи двох дискретних випадкових величин.
- •Коефіцієнт кореляції та його властивості.
- •Функція розподілу ймовірностей та щільність ймовірностей системи
- •Двовимірний нормальний закон розподілу.
- •Закон розподілу Бернулі
- •Біноміальний закон розподілу двв. Числові характеристики.
- •Пуасонівський закон розподілу двв, числові характеристики.
- •Геометричний закон розподілу двв, числові характеристики.
- •Гіпергеометричний закон розподілу двв, числові характеристики.
- •Рівномірний закон розподілу нвв.
- •Нормальний закон розподілу.
- •Показниковий закон та його використання в теорії надійності та теорії черг.
- •Розподіл
- •Розподіл Стьюдента. Розподіл Фішера. (45-46)
- •Правило трьох сигм. Логарифмічний нормальний закон.
- •Функції одного дискретного випадкового аргументу.
- •.Числові характеристики функції одного дискретного випадкового аргументу.
- •Функції неперервного випадкового аргументу та їх числові характеристики.
- •Функції двох випадкових аргументів та їх числові характеристики.
- •Числові характеристики функції дискретного випадкового аргументу
- •Нерівності Чебишева та їх значення.
- •Теорема Чебишева.
- •Теорема Бернуллі.
- •Центральна гранична теорема теорії ймовірностей ( теорема Ляпунова) та її використання у математичній статистиці.
- •Предмет і задачі математичної статистики.
- •Утворення вибірки. Генеральна та вибіркова сукупність.
- •Статистичні розподіли вибірок.
- •Емпірична функція розподілу, гістограма та полігон.
- •Числові характеристики: вибіркова середня, дисперсія вибірки, середньоквадратичне відхилення.
- •Мода й медіана, емпіричні початкові та центральні моменти, асиметрія та ексцес.
- •Дати визначення статистичної оцінки.
- •Точкові та інтервальні статистичні оцінки.
- •Дати визначення довірчого інтервалу.
- •Що таке нульова та альтернативна статистичні гіпотези.
- •Перевірка (правдивості нульової) гіпотези про нормальний закон розподілу ознаки генеральної сукупності.
- •Емпіричні та теоретичні частоти.
- •Критерії узгодження Пірсона та Колмогорова.
- •Помилки першого та другого роду.
- •Статистичний критерій. Критична область.
- •Дати означення моделі експерименту.
- •Дати поняття одно факторний аналіз.
- •Загальна дисперсія, між групова та внутрішньогрупова дисперсії.
- •. Поняття про функціональну, статистичну та кореляційну залежності.
- •Рівняння лінійної регресії. Довірчий інтервал для лінії регресії
- •Вибірковий коефіцієнт кореляції.
- •Множинна регресія, множинний коефіцієнт кореляції та його властивості.
- •Нелінійна регресія.
- •85) Визначення та приклади ланцюгів Маркова.
- •Інтуїтивне визначення
- •Формальне визначення
- •Граф переходів ланцюга Маркова
- •86) Ймовірність переходу за n кроків.
- •87) Замкнуті множини станів.
- •88) Класифікація станів. Неповоротний стан.
- •1. Ергодичний стан
- •2. Нестійкі стани
- •3. Поглинальні стани
- •89) Ергодична властивість неперіодичних ланцюгів. Стаціонарний розподіл.
- •90) Періодичні ланцюги.
- •91) Загальний марковський процес (Ланцюг Маркова з неперервним часом).
- •92) Гранична поведінка перехідних ймовірностей ланцюга Маркова.
- •93) Гілчастий процес.
- •94) Алгебраїчний підхід вивчення скінченних ланцюгів Маркова.
- •96) Випадковий проце, стаціонарний у широкому сенсі.
- •97) Аналіз кореляційної функції. Ергодичність.
- •100) Рівняння Колмогорова - Чепмена
.Числові характеристики функції одного дискретного випадкового аргументу.
1. Математичне
сподівання

2. Дисперсія
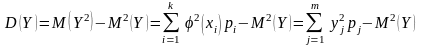
3. Середнє квадратичне
відхилення

Приклад 2. За заданим законом розподілу
Х = хi |
|
|
|
0 |
|
|
|
Р (Х = хi) = pi |
0,1 |
0,2 |
0,1 |
0,1 |
0,2 |
0,1 |
0,2 |
Обчислити М (Y),
D (Y), (Y),
якщо Y = cos2 х.
М (Y),
D (Y), (Y),
якщо Y = cos2 х.
Розв’язання. Побудуємо закон розподілу Y.
Y = cos2 хi |
|
|
|
|
|
|
|
Р (Y = cos2 хi) = pi |
0,1 |
0,2 |
0,1 |
0,1 |
0,2 |
0,1 |
0,2 |
або
Y = cos2 хi |
|
|
|
1 |
|
|
|
Р (Y = cos2 хi) = pi |
0,1 |
0,2 |
0,1 |
0,1 |
0,2 |
0,1 |
0,2 |
Y = cos2 хi |
|
|
|
1 |
|
|
|
Р (Y = cos2 хi) = pi |
0,1 |
0,2 |
0,1 |
0,1 |
0,2 |
0,1 |
0,2 |
Y = уj |
0,25 |
0,5 |
0,75 |
1 |
Р (Y = уj) = pj |
0,3 |
0,3 |
0,3 |
0,1 |

Функції неперервного випадкового аргументу та їх числові характеристики.
Нехай закон розподілу ймовірностей неперервної випадкової величини Х задано щільністю f (х).
Необхідно знайти
f (у), якщо Y =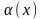 .
.
А. Функція монотонна.
Розглянемо випадок, коли Y = є монотонно зростаючою функцією, зображеною на мал. 1.
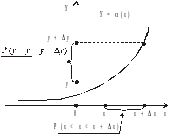
Мал. 1
Якщо випадкова величина Х міститься у проміжку [х; х + х], то оскільки Y жорстко зв’язана з випадковою величиною Х функцією (х), то Y міститиметься у проміжку [у, у + у] (мал.1). Отже, події х < Х < х +х і у < Y < у +у будуть рівноймовірними:
Р(х < Х < х +х) = Р(у < Y < у +у). (1)
Згідно з визначенням щільності ймовірностей
 .
.
Але
F( у +  у) – F(у) = Р (у < Y < у +у) = Р (х < Х < х +х)
згідно зі (1).
у) – F(у) = Р (у < Y < у +у) = Р (х < Х < х +х)
згідно зі (1).
Тоді:

Отже,
 .
(2)
.
(2)
При у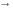 0,
х
0
з урахуванням функціональної залежності
між Y і Х, помноживши і поділивши дріб
(2) на х,
дістанемо:
0,
х
0
з урахуванням функціональної залежності
між Y і Х, помноживши і поділивши дріб
(2) на х,
дістанемо:

Із Y = (х)
знаходимо явно Х =
 (у).
Тоді
(у).
Тоді
 (3)
(3)
Якщо
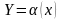 ,
де
,
де
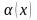 є монотонно спадною функцією (мал..2),
є монотонно спадною функцією (мал..2),

мал. 2
то додатному
приросту аргументу х +х
відповідатиме від’ємний приріст функції
y – y
i похідна
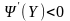 .
.
А оскільки f (y) 0,
то об’єднуючи обидва випадки, дістанемо
0,
то об’єднуючи обидва випадки, дістанемо
 (4)
(4)
Б. Загальна методика знаходження f (у).
Нехай неперервна
випадкова величина Х задана щільністю
ймовірностей f (х), якщо
 .
.
Необхідно визначити f (у), якщо , де є монотонною функцією.
1. Необхідно визначити множину можливих значень для Y
Оскільки
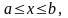 то
то
 .
.
2. Із
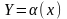 знаходимо явний вираз Х через Y, а саме:
знаходимо явний вираз Х через Y, а саме:
 .
.
3. Знаходимо похідну
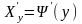 .
.
4. Будуємо щільність імовірностей для випадковой величини Y
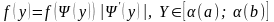 .
.
5. Перевіряється виконання умови нормування для f (у):
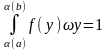 .
.
Якщо нормування виконується, то f (у) знайдено вірно.
За знайденою f (у) функцією розподілу ймовірностей визначається
 .Числові
характеристики функцій неперервного
випадкового аргументу визначаються за
формулами:
.Числові
характеристики функцій неперервного
випадкового аргументу визначаються за
формулами:
математичне сподівання
 ;
;
дисперсія

 ;
;
середнє квадратичне
відхилення
 .
.