16. Дифференцируемость функций. Производная постоянной, произведения постоянной на функцию,суммы, произведения и частного двух функций.

17. Неявная функция и ее дифференцирование

18. Обратная функция и ее дифференцирование.

19. Параметрическое задание функции. Производная функции, заданной параметрически

20. Дифференциал функции. Понятие дифференциала, его геометрическое значение

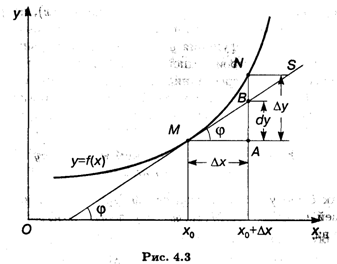
Дифференциалом функции у = F(X) в точке X0 называется главная линейная относительно ΔX часть приращения функции в этой точке

Дифференциал функции имеет четкий геометрический смысл (рис. 4.3). Пусть точка М на графике функции У = F{X)соответствует значению аргумента X0, точка N — зна­чению аргумента X0 + ΔX, MS — касательная к кривой F(X) в точке М, φ — угол между касательной и осью Ох. Тогда МА — приращение аргумента, AN — соответствующее при­ращение функции. Рассматривая треугольник АВМ, получа­ем, что АВ = ΔX tg φ = F'(X0) ΔX = Dy, т. е. это главная по по­рядку величины ΔX и линейная относительно нее часть прира­щения функции ΔУ. Оставшаяся часть более высокого порядка малости соответствует отрезку BN.

21. Производные различных порядков. Дифференциалы различных порядков

Пусть функция y = f(x) дифференцируема на некотором отрезке [a, b]. Значения производной f ў(x), вообще говоря, зависят от x, т.е. производная fў(x) представляет собой тоже функцию от x. При дифференцировании этой функции получается так называемая вторая производная от функцииf(x), которая обозначается f ўў (x).

Производной n-го порядка от функции f(x) называется производная (первого порядка) от производной n-1-го и обозначается символом y(n) = (y(n – 1))ў.

Дифференциалы различных порядков.

Дифференциал функции y = f(x), где x – независимая переменная, есть dy= f ў(x)dx, некоторая функция от x, но от x может зависеть только первый сомножитель f ў(x), второй же сомножитель (dx) является приращением независимой переменной x и от значения этой переменной не зависит. Так как dy есть функция от x, то можно определить дифференциал этой функции. Дифференциал от дифференциала функции называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d2y:

d(dx) = d2y = f ўў(x)(dx)².

Дифференциалом n-го порядка называется первый дифференциал от дифференциала n-1-го порядка:

dⁿy = d(dⁿ–1 y) = f(n)(x)dx(n).

22. Уравнение касательной и нормали к кривой. Угол между двумя пересекающимися кривыми.

Уравнение нормали – х - х₀ + y'(х₀)( y-у₀) = 0

Уравнение касательной – y-у₀ = y'(х₀)(x - x₀)

Углом между кривыми на плоскости в их общей точке называется наименьший из двух возможных углов между касательными к этим кривым в данной точке.

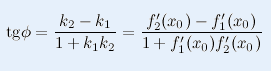
23, Некоторые теоремы о дифференцируемых функциях. Теорема о корнях производной (Ролля). Теорема о

конечных приращениях (Лагранжа). Теорема об отношении приращений двух функций (Коши).

24. Предел отношения двух бесконечно малых величин (теорема Лопиталя).

25. . Формула Тейлора. - Формула Тейлора

, где R_n(x) - остаточный член формулы Тейлора.

26 Разложение по формуле Тейлора функций ex, sin(x), cos(x), ln(1+x), (1+x)m.

можно выполнить исходя из 25 вопроса Задание. Разложить в ряд Тейлора функцию   в точке  .

Решение. Найдем производные:

Итак,  ,  ,  . Значение функции в точке

Таким образом,

Ответ. 

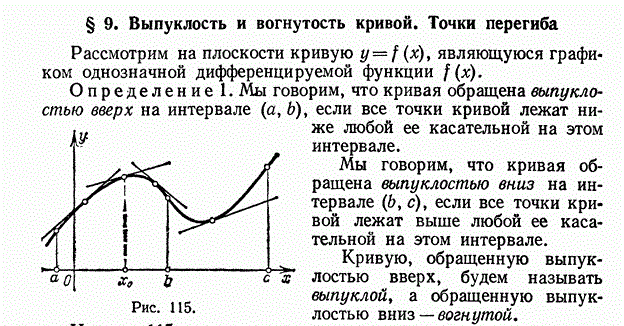
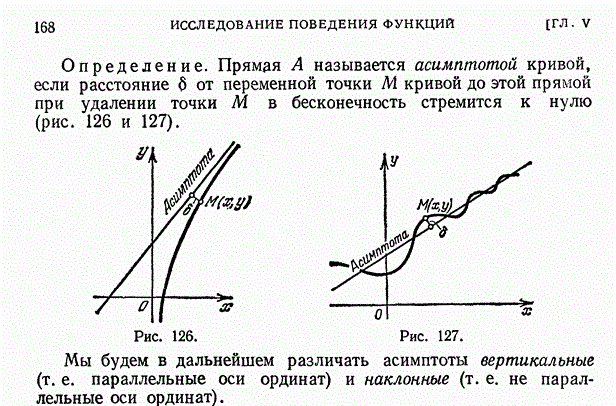
27. Исследование поведения функций при помощи производной. Возрастание и убывание функций, максимум и минимум функций. Выпуклость и вогнутость кривой. Точки перегиба. Асимптоты

28. Наибольшее и наименьшее значение функции на отрезке

Точка максимума (с + на )

Точка минимума (с - на + )

Запишем алгоритм, позволяющий находить наибольшее и наименьшее значение функции на отрезке.

1. Находим область определения функции и проверяем, содержится ли в ней весь отрезок [a;b].

2. Находим все точки, в которых не существует первая производная и которые содержатся в отрезке [a;b] (обычно такие точки встечаются у функций с аргументом под знаком модуля и у степенных функций с дробно-рациональным показателем). Если таких точек нет, то переходим к следующему пункту.

3. Определяем все стационарные точки, попадающие в отрезок [a;b]. Для этого,находим производную функции, приравниваем ее к нулю, решаем полученное уравнение и выбираем подходящие корни. Если стационарных точек нет или ни одна из них не попадает в отрезок, то переходим к следующему пункту.

4. Вычисляем значения функции в отобранных стационарных точках (если такие имеются), в точках, в которых не существует первая производная (если такие имеются), а также при x=a и x=b.

5. Из полученных значений функции выбираем наибольшее и наименьшее - они и будут искомыми наибольшим и наименьшим значениями функции соответственно.