27.3. Интегрирование линейных однородных уравнений n-го порядка с постоянными коэффициентами

Полученные результаты для решения линейного однородного уравнения второго порядка с постоянными коэффициентами обобщаются на случай уравнения n-го порядка следующим образом.

Рассмотрим линейное однородное уравнение с постоянными коэффициентами (2):

.

• Характеристическим уравнением для уравнения (2) называется алгебраическое уравнение n-го порядка вида:

. (5)

Уравнение (5) имеет ровно n корней (считая кратные и комплексно сопряженные корни). А именно, левая часть уравнения (5) раскладывается на множители первого и второго порядка, так что уравнение принимает вид:

(причем , и ).

Здесь =_j – действительные корни уравнения (3) кратности k_­j

(j=1,..,m),

(где - мнимая единица) – пары комплексно сопряженных корней кратности s_j (j=1,…,l).

Каждому корню характеристического уравнения (5) соответствует элемент фундаментальной системы решений по следующему правилу:

Корень уравнения (3)	Кратность корня	Соответствующие элементы фундаментальной системы решений
1 – действительный корень	1
	2
	3
	…
1,2=i – два комплексно сопряженных корня	1
	2
	…

Общее решение уравнения (2) имеет вид .

Пример 1.

Характеристическое уравнение:

;

₁=0 – действительный корень кратности 1, следовательно,

₃=-1 – действительный корень кратности 2, следовательно,

.

Таким образом, общее решение данного уравнения:

.

Пример 2.

Характеристическое уравнение:

;

₁=0 – действительный корень кратности 2, следовательно,

- два комплексно сопряженных корня кратности 1, следовательно,

.

Таким образом, общее решение:

.

Пример 3.

Характеристическое уравнение:

;

;

- два комплексно сопряженных корня кратности 2, следовательно,

.

Таким образом, общее решение:

.

27.4. Неоднородные линейные уравнения с постоянными коэффициентами

Теорема 27.2. (о структуре общего решения):

Общим решением у линейного уравнения с постоянными коэффициентами

(1)

является сумма его произвольного частного решения и общего решения соответствующего однородного уравнения: .

Теорема 27.3. (о наложении решений):

Если правая часть уравнения (1) представляет собой сумму двух функций: , а и - частные решения уравнений и

,

то - частное решение уравнения (1).

27.5. Метод вариации произвольных постоянных

Частное решение уравнения (1) можно найти при помощи метода вариации произвольных постоянных.

Пусть найдено общее решение соответствующего однородного уравнения (2):

.

Тогда функция

,

где функции удовлетворяют системе уравнений

будет решением уравнения (1).

Пример.

Найдем общее решение соответствующего однородного уравнения:

.

;

- два комплексно сопряженных корня кратности 1, следовательно, общее решение: .

Тогда частное решение исходного уравнения имеет вид

,

где

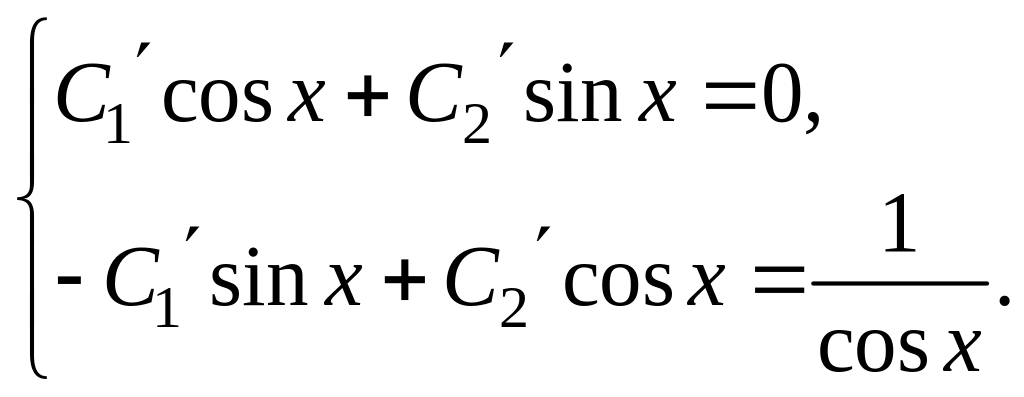
Разрешая систему относительно С₁´ и С₂´, получаем

,

откуда интегрированием находим

.

Согласно теореме о структуре решения неоднородного линейного уравнения, получаем общее решение данного уравнения:

.