§26. Оду высших порядков

26.1. Основные понятия

Обыкновенное дифференциальное уравнение n-го порядка имеет вид:

(1)

или, если оно разрешено относительно старшей производной:

(2)

Решением ОДУ (2) называется любая функция , которая при подстановке в уравнение обращает его в тождество.

Как и для уравнения первого порядка, задачей Коши для уравнения (2) называется задача нахождения решения уравнения (2), удовлетворяющего начальным условиям

. (3)

Теорема 26.1. (существования и единственности решения задачи Коши):

Если в уравнении (2)функция непрерывна вместе со своими частными производными 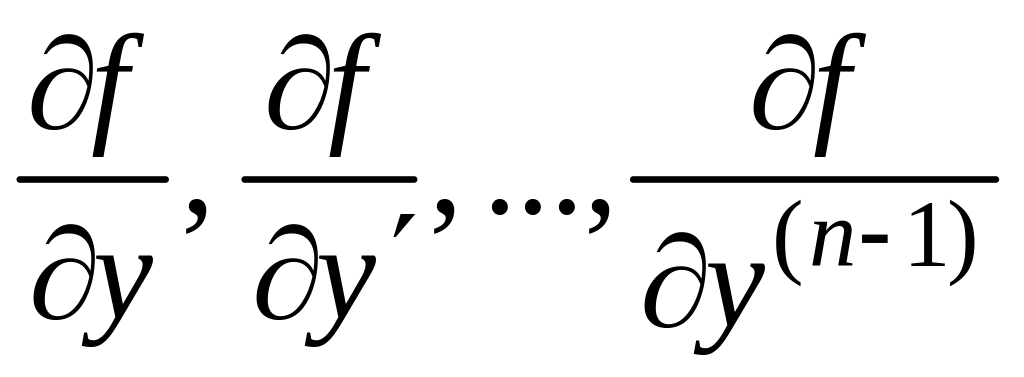в некоторой области D изменения переменных , то для всякой точки существует единственное решение задачи (2),(3).

Общим решением уравнения (2) называется функция , где С₁,…,C_n – произвольные постоянные, удовлетворяющая условиям:

1) является решением ОДУ (2) при любом наборе постоянных С₁,…,C_n,

2) любое решение задачи Коши (2),(3) имеет вид при некоторых значениях постоянных С₁,…,C_n.

Уравнение вида , которое определяет общее решение дифференциального уравнения (2) в неявном виде, называют общим интегралом этого уравнения.

Решение уравнения (2), получающееся из общего при некотором наборе постоянных С₁,…,С_n, называется частным решением. График частного решения называется интегральной кривой данного дифференциального уравнения.

26.2. Уравнения, допускающие понижение порядка

Одним из методов интегрирования ОДУ высших порядков, является метод понижения порядка уравнения. Рассмотрим некоторые виды дифференциальных уравнений, допускающих понижение порядка.

I. Уравнение вида

Общее решение таких уравнений получается последовательным n-кратным интегрированием.

Пример.

Интегрируя последовательно данное уравнение, имеем:

;

;

.

Поскольку значение постоянной С_1­ никак не связано со значениями остальных слагаемых в полученном общем решении, обозначим .

Таким образом, общее решение: .

II. Уравнение вида ,

не содержащее искомой функции и первые k-1 ее производных.

Порядок такого уравнения можно понизить заменой неизвестной функции . Тогда уравнение принимает вид .

Находим, если возможно, решение последнего уравнения в виде , а затем последовательным интегрированием уравнения находим общее решение исходного уравнения.

Пример.

Данное уравнение не содержит искомой функции у и ее производной. Полагая , получаем уравнение 1 порядка:

.

Решаем полученное уравнение:

.

Выражаем в явном виде р:

.

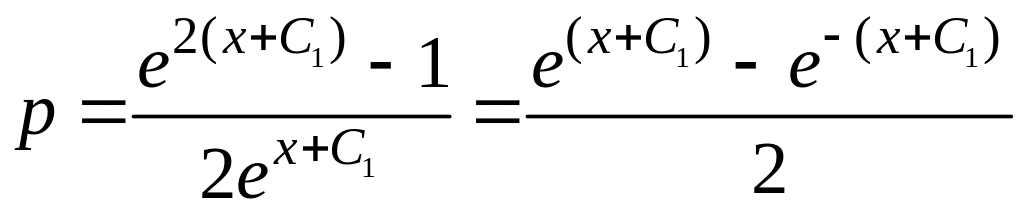Возвращая старую функцию у, имеем:

;

;

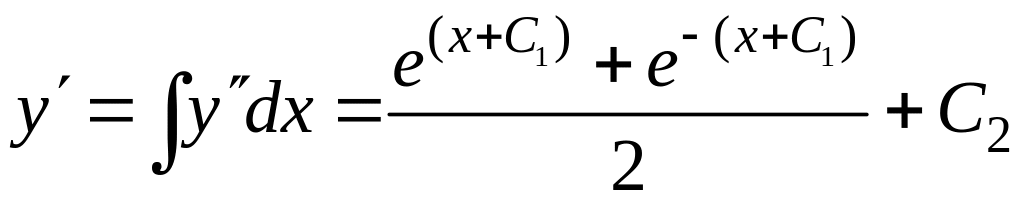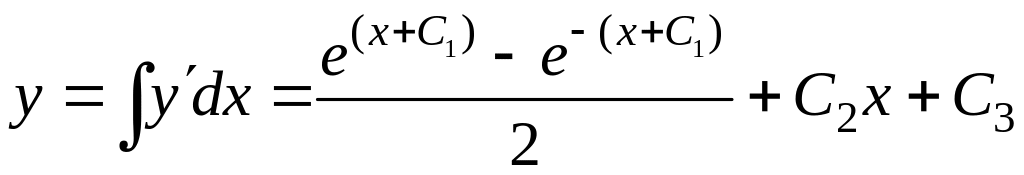- общее решение исходного уравнения.

III. Уравнение вида ,

не содержащее независимого переменного.

Порядок уравнения можно понизить на единицу при помощи подстановки . Выразим все производные через производные от новой неизвестной функции р(у) по у:

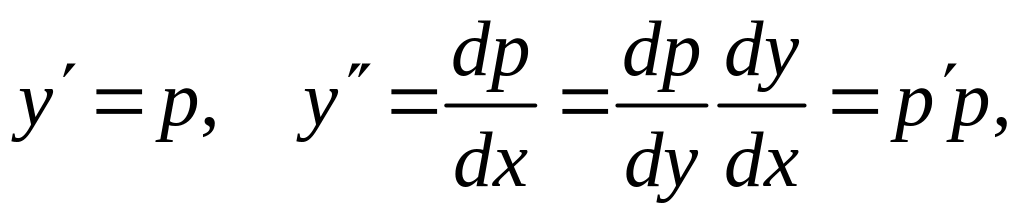
и т.д.

Подставляя эти выражения в исходное уравнение, получаем уравнение (n-1)-го порядка относительно неизвестной функции р(у). Если возможно, находим его общее решение . Далее, решая уравнение с разделяющимися переменными находим общее решение исходного уравнения.

Пример.

Уравнение не содержит независимой переменной х.

Положим :

, или

. (*)

Получили уравнение Бернулли. Оно сводится к линейному подстановкой

:

;

. (**)

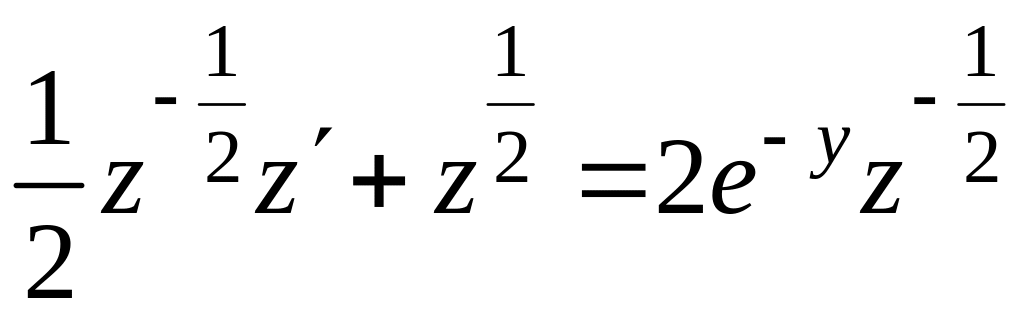Решаем соответствующее однородное линейное уравнение:

.

Применяем метод вариации произвольной постоянной:

;

таким образом, общее решение уравнения (**) имеет вид , тогда общее решение уравнения (*): .

Заменяя , получаем уравнение с разделяющимися переменными относительно у(х):

.

Разделяя переменные и интегрируя, получаем:

,

откуда получаем общее решение исходного уравнения в виде

(здесь ).

Замечание. При решении задачи Коши для уравнений высших порядков целесообразно определять значения произвольных постоянных в процессе решения, а не после нахождения общего решения уравнения. Это ускоряет решение задачи и, кроме того, интегрирование при произвольных постоянных часто затруднительно или даже невозможно.

Пример.

Уравнение не содержит независимой переменной.

Полагаем :

.

Таким образом, . Это уравнение с разделяющимися переменными, однако интеграл в общем случае не берется.

Используем начальные условия:

, то есть , откуда С₁=0, а знак следует выбрать «+».

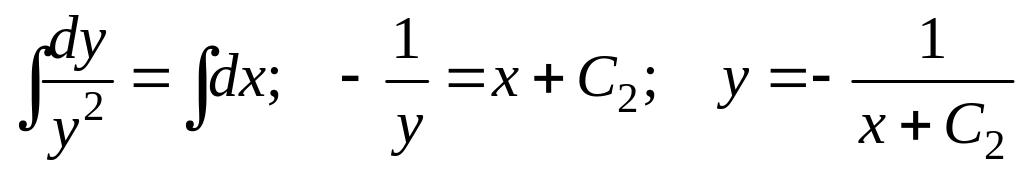Следовательно, для данной задачи , откуда получаем . Используя начальное условие, находим С₂=-1, следовательно, искомое решение задачи Коши: .