25.4. Однородные уравнения
Дифференциальное уравнение вида
(3)
называется однородным уравнением.
Однородное
уравнение при помощи замены функции
или
приводится к уравнению с разделяющимися
переменными. Действительно, тогда
dy=tdx+xdt.
Уравнение
после замены принимает вид
или
.
Пример:
Сделаем замену , тогда dy =tdx+xdt. Уравнение примет вид
,
или
.
Разделяем
переменные:
.
Интегрируя,
получаем общее решение
или
,
откуда
.
Поскольку
линии х=0
и t=0
не входят в область существования
уравнения, следует проверить только,
не было ли при разделении переменных
потеряно решение t=е,
на котором обращается в ноль выражение
.
При подстановке в уравнение и в общее
решение убеждаемся что t=е
является частным решением уравнения,
получающемся из общего при С=0.
Таким
образом, получили решение в виде
.
Подставляя выражение для t,
получаем общее решение исходного
уравнения:
.
Замечание.
Уравнение вида
или
является однородным, если функции (х,у)
и (х,у)
являются однородными
функциями
одной и той же степени n,
то есть
.
Для того, чтобы привести это уравнение
к виду (3), следует разделить обе части
уравнения на хn.
Пример.
Функции
x
и
являются однородными степени 1. Умножим
исходное уравнение на dx
и
разделим на х
(заметим при этом, что х=0
не является решением исходного уравнения):
-
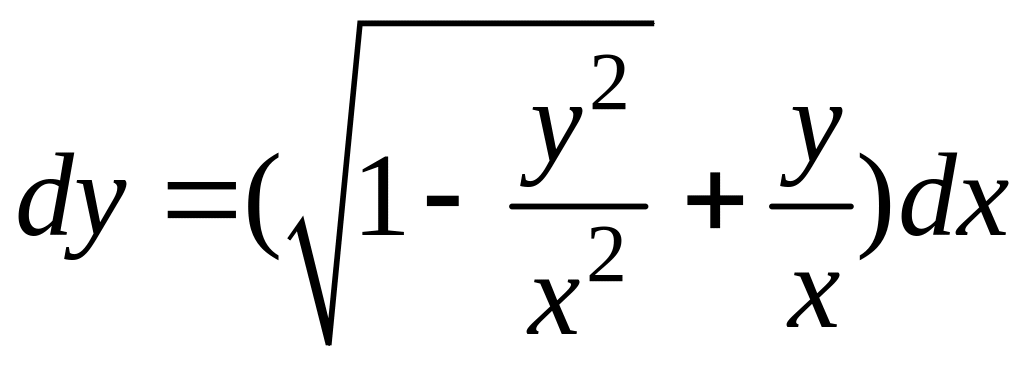однородное уравнение.
Сделав замену , получаем уравнение с разделяющимися переменными:
;
.
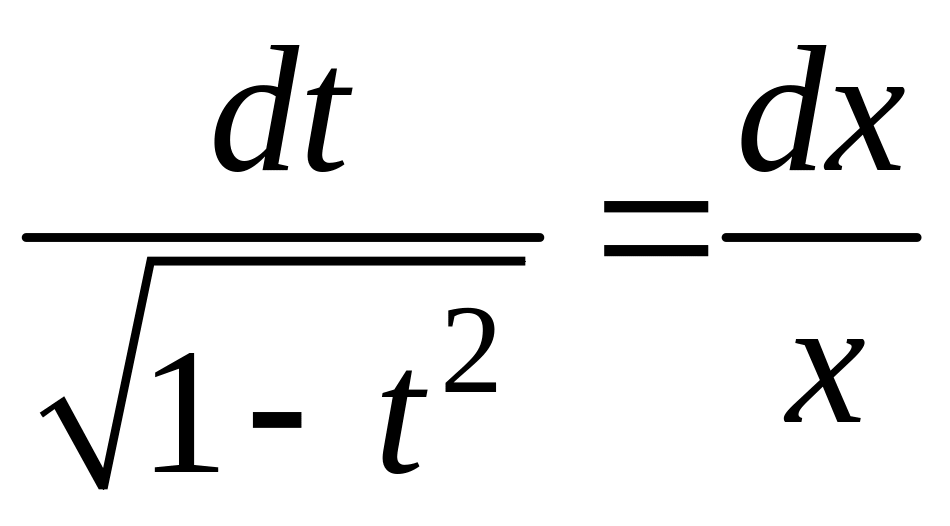Интегрируя, получаем общее решение
или
(где С=
),
откуда
.
При
разделении переменных мы делили обе
части уравнения на
,
считая, что это выражение не равно 0.
Непосредственной подстановкой в
уравнение и в общее решение убеждаемся,
что функции t=1
являются особыми решениями уравнения.
Возвращая старую функцию y=tx, получаем окончательно:
общее
решение исходного уравнения
и особые решения y=x.
Замечание.
Уравнения
вида
преобразуются в однородные путем замены
переменных
,
где
и
подбираются
таким образом, чтобы после замены
уравнение приняло вид
,
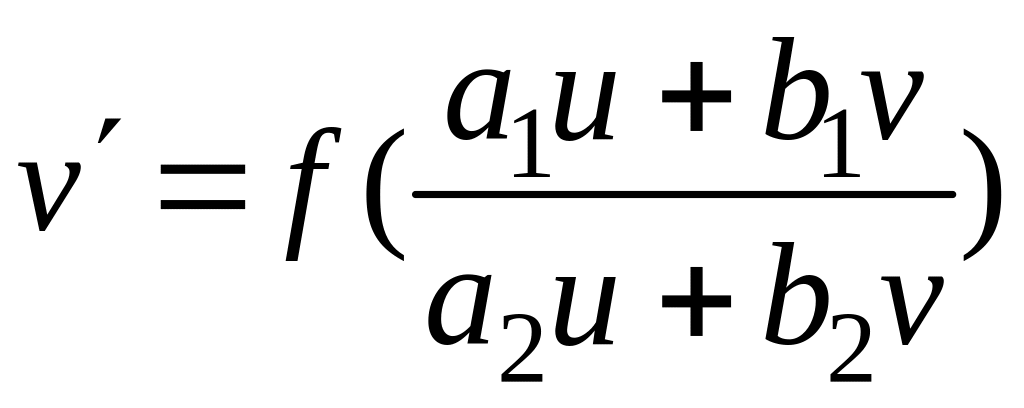то есть
.
Пример.
Найти общий интеграл уравнения
.
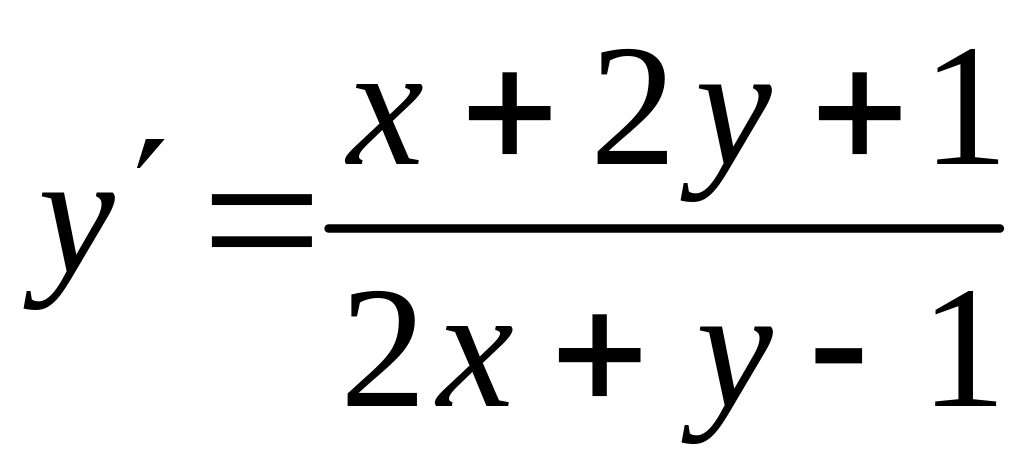Положим , получаем:
.
Подберем
и
так, чтобы
Находим:
=1,
=-1.
Таким
образом, получаем однородное уравнение
.
Для
его решения положим
:
;
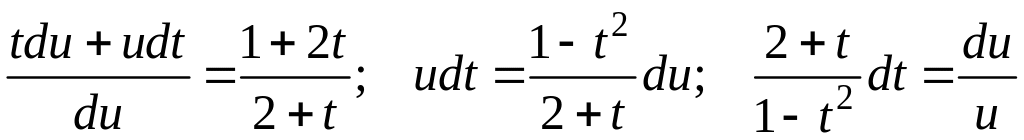интегрируя последнее уравнение, получаем:
,
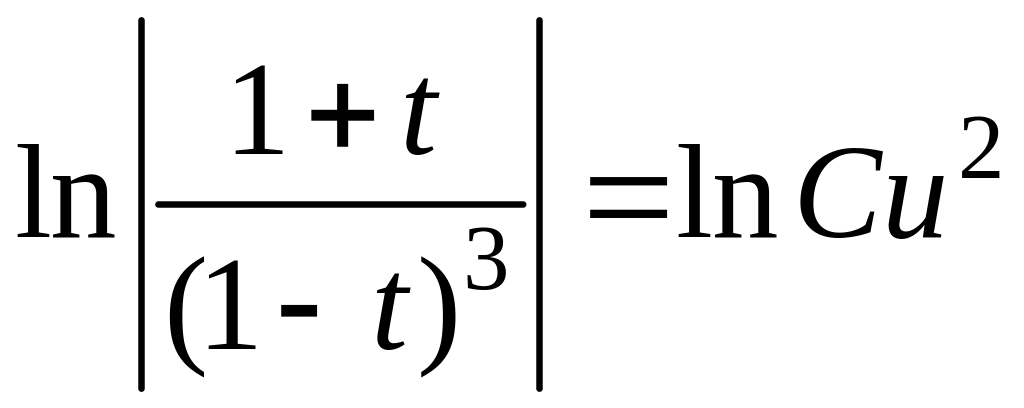или
.
Возвращаем
:
,
откуда
.
Заменяем
,
получаем общий интеграл исходного
уравнения:
.
25.5. Линейные уравнения первого порядка
Дифференциальное уравнение вида
(4)
называется линейным дифференциальным уравнением первого порядка.
Особенность этого уравнения в том, что оно линейно относительно неизвестной функции и ее производной, т.е. у и у´ входят в это уравнение в первой степени (и не перемножаются между собой).
При b(x)=0 уравнение (4) принимает вид
(5)
и называется линейным однородным уравнением первого порядка.
Однородное линейное уравнение (5) является также уравнением с разделяющимися переменными и может быть решено следующим образом:
;
;
;
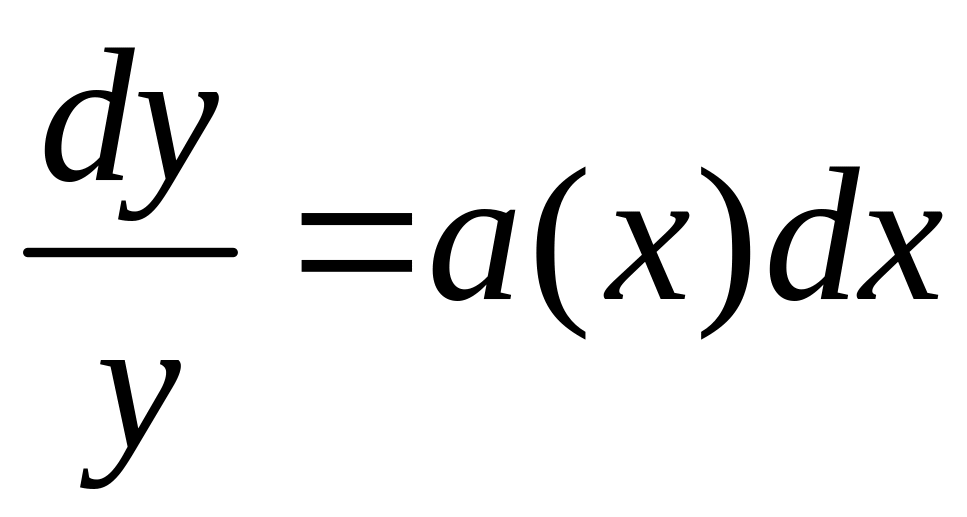(6)
Для решения уравнения (4) применяют метод вариации произвольной постоянной. При этом решение уравнения (4) ищут в виде (6), считая, что С=С(х) – некоторая функция. Подставляем это выражение в (4):
так
как
,
причем
,
то получаем
,
или
,
откуда находим С(х):
.
Таким образом, общее решение уравнения (3) имеет вид
.
Пример 1.
Имеем линейное уравнение. Решим соответствующее линейное однородное уравнение:
.
Воспользуемся
методом вариации произвольной постоянной:
будем искать решение исходного уравнения
в виде
.
Подставим это выражение для у в уравнение
и найдем неизвестную функцию С(х):
;
;
.
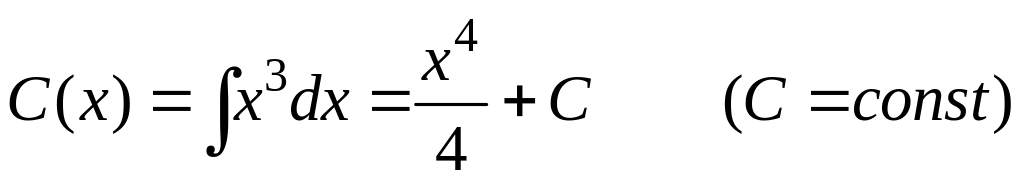Таким
образом, общее решение исходного
уравнения имеет вид:
.
Пример 2.
Данное
уравнение не является линейным
относительно неизвестной функции у(х).
Однако мы можем рассматривать х
как функцию аргумента у,
при этом
и уравнение принимает вид
,
то есть является линейным относительно неизвестной функции х(у). Решим соответствующее линейное однородное уравнение:
.
Воспользуемся методом вариации произвольной постоянной:
;
;
;
.
Следовательно, общее решение исходного уравнения имеет вид
.