28.3. Элементы теории устойчивости

Рассмотрим систему дифференциальных уравнений

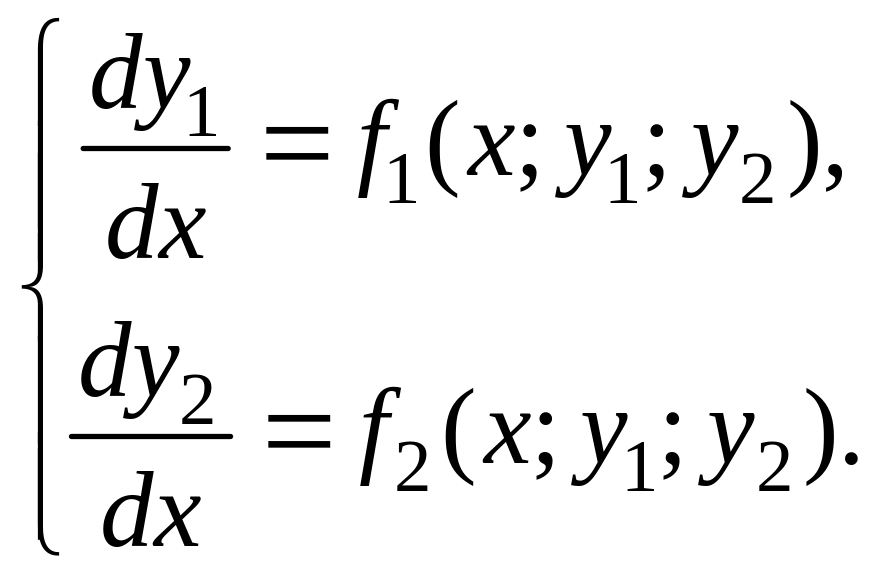(1)

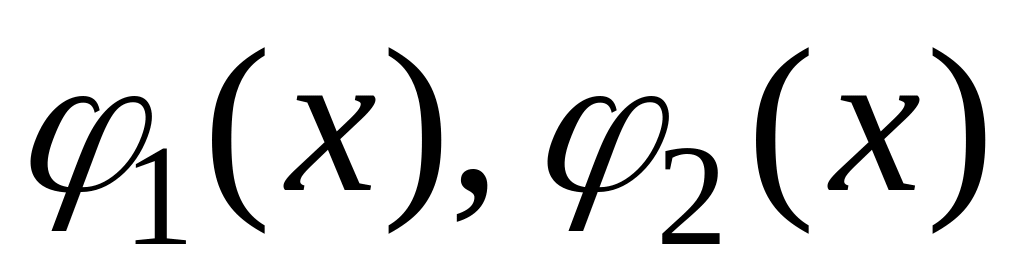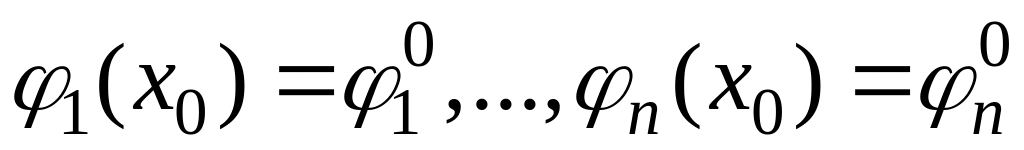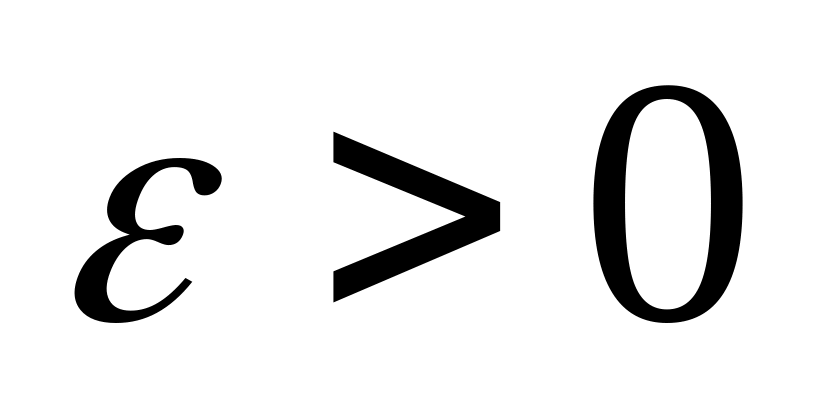• Решение системы (1), удовлетворяющее начальным условиям называется устойчивым по Ляпунову, если для любого существует число такое, что для всякого решения системы (1), начальные значения которого удовлетворяют условиям

, (2)

имеют место неравенства

(3)

для всех .

Проще говоря, решение является устойчивым по Ляпунову, если малое отклонение начальных условий приводит к малому отклонению решения.

• Если при сколь угодно мало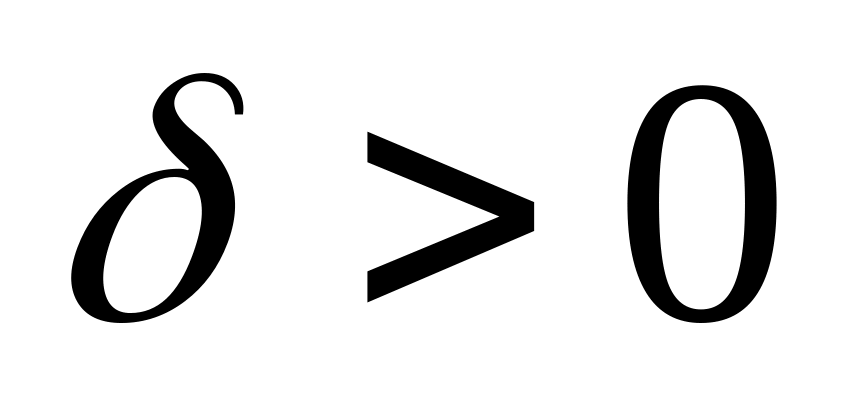м хотя бы для одного решения неравенства (3) не выполняются, то решение называется неустойчивым.

• Если, кроме выполнения неравенств (3) при условии (2) выполняется также условие

, (4)

то решение называется асимптотически устойчивым.

Исследование на устойчивость решения системы (1) может быть при помощи подстановки сведено к исследованию на устойчивость нулевого (тривиального) решения некоторой системы, аналогичной системе (1):

(1´)

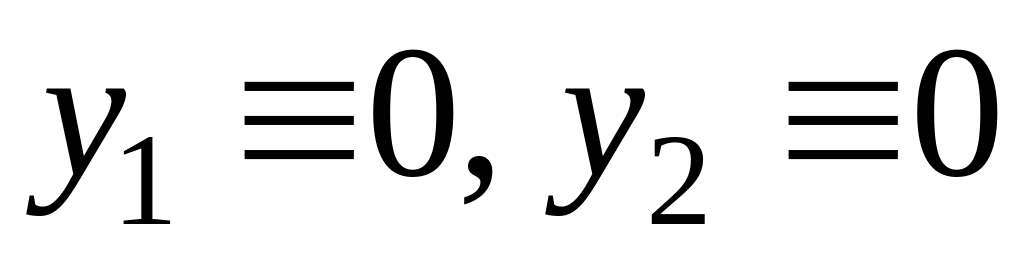• Решение называется точкой покоя системы (1´).

Сформулируем определения устойчивости применительно к точке покоя.

• Точка покоя системы (1´), называется устойчивой по Ляпунову, если для любого 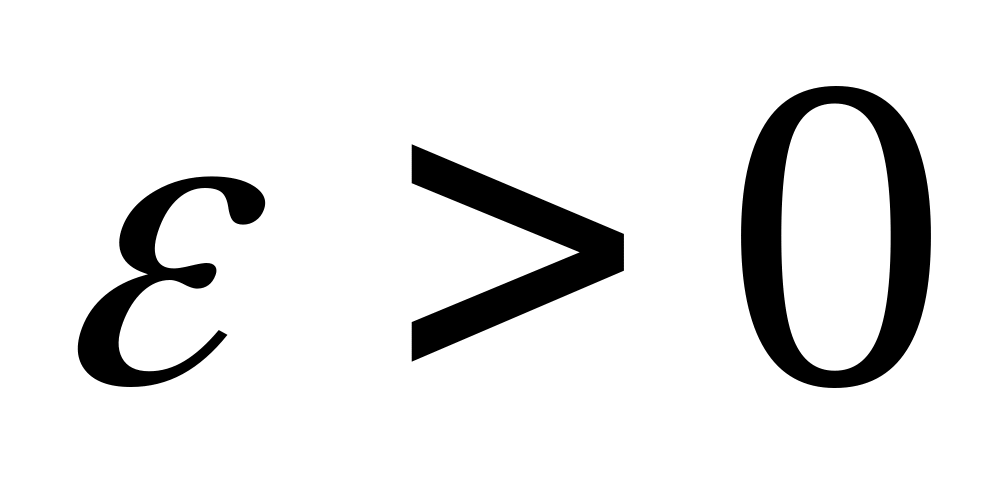существует число такое, что для всякого решения системы (1), начальные значения которого удовлетворяют условиям

, (2´)

имеют место неравенства

(3´)

для всех .

Геометрически это означает, что каким бы узким ни был цилиндр радиуса  с осью Ох, найдется -окрестность точки (0;0;х₀) такая, что все интенгральные кривые, выходящие из этой окрестности, для всех будут оставаться внутри этого цилиндра.

• Если, кроме выполнения неравенств (3´), выполняется также условие

, (4´)

то точка покоя называется асимптотически устойчивой.

• Если при сколь угодно малом хотя бы для одного решения неравенства (3´) не выполняются, то решение называется неустойчивой.

Есть простая физическая аналогия для понятия устойчивости. Рассмотрим обычный шарик. Возможны три типа положений покоя для шарика: на плоскости, в нижней точке впадины, в верхней точке выпуклости. Легко видеть, что первое положение покоя устойчиво, второе – асимптотически устойчиво, третье – неустойчиво.

28.4. Простейшие типы точек покоя

Рассмотрим систему двух линейных однородных дифференциальных уравнений с постоянными коэффициентами:

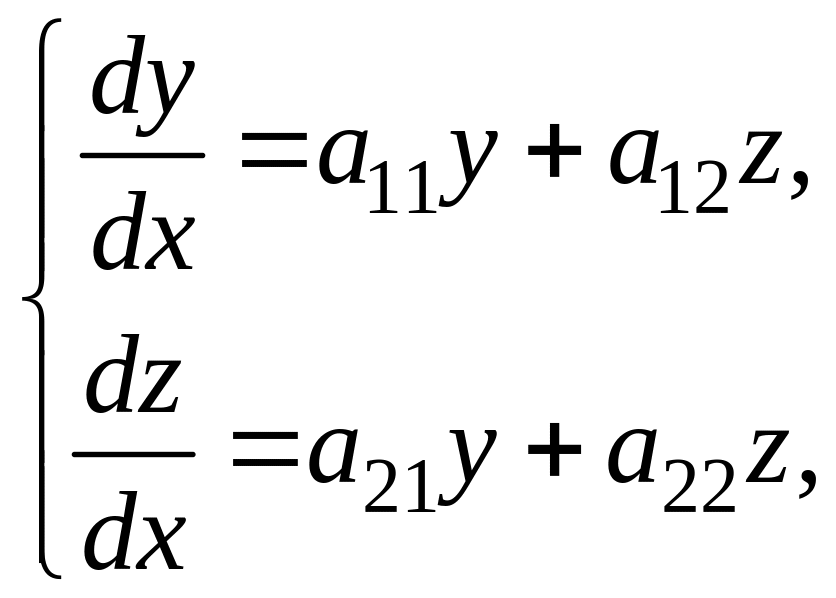(5)

причем .

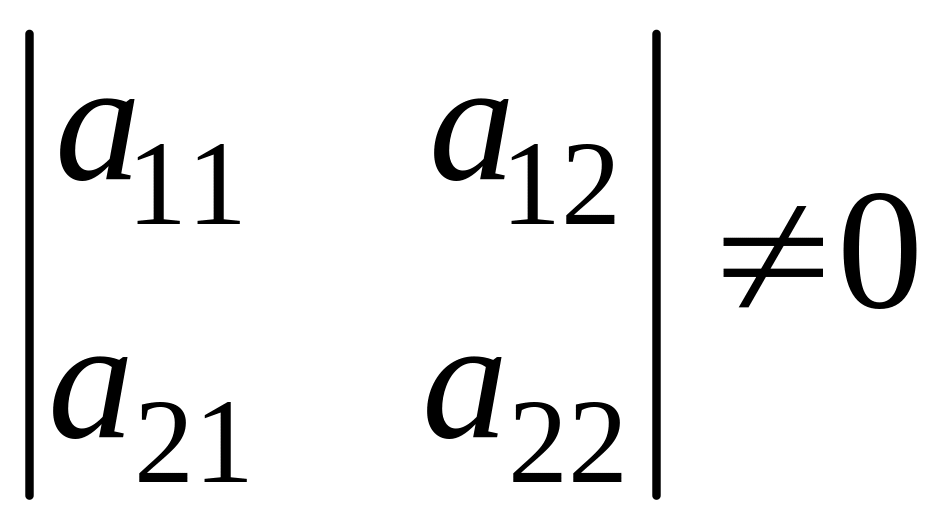Решение y=0, z=0 называется точкой покоя или особой точкой системы (5).

Составим характеристическое уравнение системы (5):

(6)

и найдем его корни ₁, ₂.

Возможны следующие случаи:

1. Корни характеристического уравнения (6) вещественные и различные:

а) . Точка покоя асимптотически устойчива (устойчивый узел).

б) . Т очка покоя неустойчива (неустойчивый узел).

в) . Точка покоя неустойчива (седло).

(На рисунках изображен «вид снизу» на интегральные кривые; стрелки указывают направление кривых при возрастании х.)

2. Корни характеристического уравнения (6) комплексные:

.

а) . Точка покоя асимптотически устойчива (устойчивый фокус).

б) . Т очка покоя неустойчива (неустойчивый фокус).

в) . Точка покоя устойчива (центр).

3. Корни кратные:

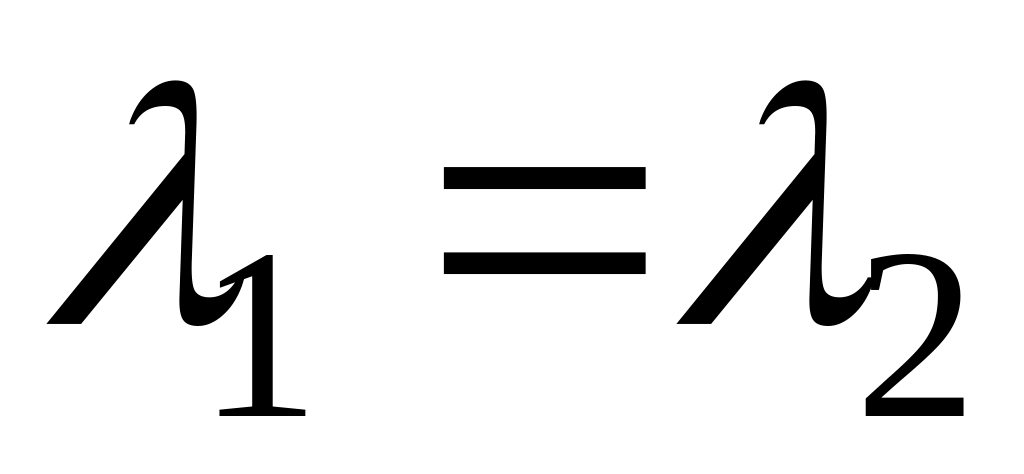
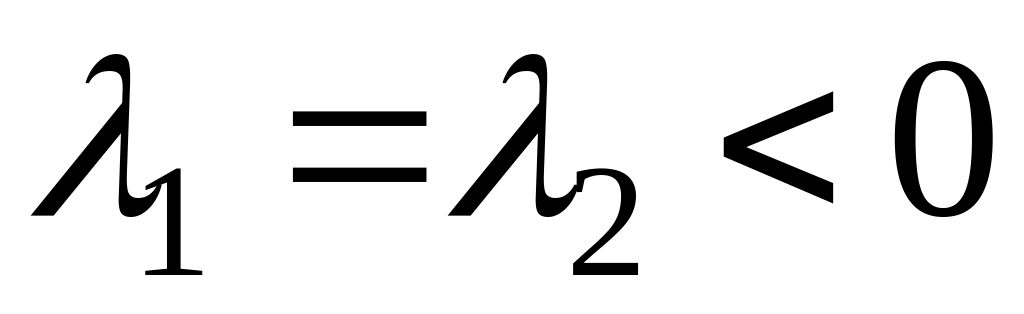
а) Точка покоя асимптотически устойчива (устойчивый узел)

б) Точка покоя неустойчива (неустойчивый узел)

77