24. Разбиение перестановки на циклы по k элементов.

Перестановка p m-множества M называется циклом, если p(x₁)=x₂, p(x₂)=x₃, …, p(x_m-1)=x_m, p(x_m)=x₁, где x₁, x₂, x₃, …, x_m-1, x_m – все, различные, элементы множества M. Этот цикл обозначается через (x₁x₂x₃…x_m-1x_m). Каждая перестановка состоит из конечного числа циклов, и эту перестановку можно записать в виде произведения циклов.

Пример. Перечислим все перестановки множества {1,2,3,4}, разбиваемые на 2 цикла:

(1)(234); (1)(243);

(2)(134); (2)(143);

(3)(124); (3)(142);

(4)(123); (4)(132);

(12)(34); (13)(24); (14)(23).

Числом Стирлинга первого рода (без знака) (или s(n,k)) называется число разбиений n-множества B на k циклов.

Приведем рекуррентные формулы для числа Стирлинга первого рода

;

, где n>0;

, где n>0, 1£k£n.

k n	0	1	2	3	4	5	6	7
0	1
1	0	1
2	0	1	1
3	0	2	3	1
4	0	6	11	6	1
5	0	24	50	35	10	1
6	0	120	274	225	85	15	1
7	0	620	1764	1624	735	175	21	1

Ясно, что .

25. Разбиение множества на блоки по k элементов.

Говорят, что семейство множеств {M₁,…,M_k} является разбиением множества M на k блоков M₁,…,M_k, если M₁,…,M_k – непустые, попарно не пересекающиеся, подмножества множества M и объединение множеств M₁,…,M_k есть множества M. Число (или S(n,k)) всех разбиений n-множества M на k блоков называется числом Стирлинга второго рода.

Пример. Перечислим все разбиения множества {1,2,3,4} на 2 блока:

{{1}, {2, 3,4}},

{{2}, {1, 3,4}},

{{3}, {1, 2,4}},

{{4}, {1, 2,3}},

{{1,2}, {3,4}},

{{1,3}, {2,4}},

{{1,4}, {2,3}}

Мы видим, что .

Приведем рекуррентные формулы для числа Стирлинга второго рода:

;

, где n>0;

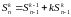, где n>0, 1£k£n.

Непосредственно число Стирлинга второго рода вычисляется по следующей формуле: .

k n	0	1	2	3	4	5	6	7
0	1
1	0	1
2	0	1	1
3	0	1	3	1
4	0	1	7	6	1
5	0	1	15	25	10	1
6	0	1	31	90	65	15	1
7	0	1	63	301	350	140	21	1

Число всех разбиений n-множества M называется числом Белла B_n.

Ясно, что .

Примечание 1. Пусть |A|=m, |B|=n. Тогда число элементов:

• множества всех отображений множества A в B равно числу всех размещений с повторениями по m из n, то есть |B^A|=n^m;

• множества всех инъекций множества A в B равно числу всех размещений без повторений по m из n, то есть ;

• множества всех биекций множества A на B равно числу всех размещений без повторений по m из n, то есть n!;

• множества всех сюръекций множества A на B равно произведению числа всех перестановок n-множества B на число всех разбиений n-множества B на m блоков, то есть n! .

Любой многочлен от одной переменной можно представить как линейную сумму степеней переменной (базисных многочленов): , , , …

Примечание 2. Определим многочлены , , которые также являются базисными: .

Связь между двумя базисными многочленами устанавливается при помощи чисел Стерлинга первого и второго родов:

, .

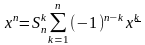Вместо «убывающих степеней» можно рассматривать «возрастающие степени»: .

, .