35. Полные графы. Граф k4 планарный и граф k5 не планарный.

Максимальным планарным графом называется планарный граф, который при добавлении любого ребра перестает быть планарным.

Из определения следует, что в максимально планарном графе все грани являются треугольниками (гранями с тремя вершинами):

если грань содержит четырехугольник (или многоугольник с большим числом сторон), то можно добавить ребро , не меняющее планарность графа, но лишающее свойства графа быть максимально планарным графом.

Пример. В следующий граф можно добавить только одно ребро, после которого этот граф обращается в граф .

Лемма. Если – планарный -граф и , то

.

Доказательство. Наибольшим числом ребер в плоском графе обладает граф, у которого все грани – треугольники. В максимальном планарном графе все грани – треугольники. Подставим в (2) . Получим .

Теорема. Графы не планарный.

Доказательство. Если (5,10)-граф планарный, то не выполняется лемма: .

36. Двудольные графы. Граф k2,3 планарный и граф k3,3 не планарный.

Граф называется двудольным -графом, если множество вершин состоит из двух непустых частей , ( , ), внутри которых нет ребер.

Если при этом все вершин из соединены со всеми вершинами из , то граф называется полным двудольным -графом и обозначается через .

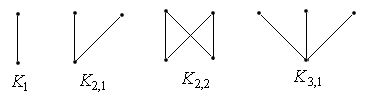
Приведем полные двудольные графы с числом вершин не больше 4:

Максимальным планарным двудольным графом называется планарный двудольный граф, который при добавлении любого ребра перестает быть планарным двудольным графом.

Если – максимальный планарный двудольный граф, то каждая ее грань является четырехугольником:

Пример. В следующий граф можно добавить только одно ребро, после которого этот граф обращается в граф :

Лемма. Если – планарный двудольный граф, то -граф, то

.

Доказательство. Наибольшим числом ребер в плоском двудольном графе обладает граф, у которого все грани – четырехугольники. В максимальном планарном графе все грани – четырехугольники. Подставим в (2) . Получим .

Теорема. Графы и не планарные.

Доказательство. Если (6,9)-граф планарный, то не выполняется лемма: .

37. Деревья. Теорема об эквивалентных определениях дерева.

Дерево – это граф, в котором выполняются любые два условия из трех условий следующей теоремы.

Теорема. Пусть для (p,q)-графа G рассматриваются три условия:

(1) G – связный граф;

(2) G – ациклический граф;

(3) p=q+1.

Тогда каждое из условий (1) – (3) следует из двух других.

Доказательство. (1), (2) Þ (3). Докажем методом математической индукции по числу ребер q. При q=1 и q=2 утверждение теоремы легко проверить. Если q³3, то удалим одно из серединных ребер. Тогда граф G разбивается на 2 подграфа – (p₁,q₁)-граф G₁ и (p₂,q₂)-граф G₂, p=p₁₊p₂, q=q₁₊q₂₊1. Так как q_1<q, q_2<q, то по индуктивному предположению, p₁₌q₁₊1, p₂₌q₂₊1, откуда p=p₁₊p₂₌q₁₊1+q₂₊1=(q₁₊q₂₊1)+1=q+1.

(1), (3) Þ (2). Докажем методом от противного. Допустим, что граф G содержит цикл с s вершинами и с s ребрами. Каждый из оставшихся p-s вершин присоединяется к этому циклу или к ранее присоединенному ребру "новым", "своим" ребром. Получается, что q не меньше суммы s+(p-s)=p, что противоречит условию (3). Значит, граф G не содержит циклов.

(2), (3) Þ (1). Докажем методом от противного. Допустим, что граф G состоит из k компонент связности (k³1). Каждая из них будет связным ациклическим графом G₁, …, G_k, соответственно с p₁,…,p_k вершинами и q₁,…,q_k ребрами, p=p₁₊…+p_k, q=q₁₊…+q_k. Для графов G₁, …, G_k имеем k равенств: p₁₌q₁₊1, …, p_k=q_k+1. Отсюда p=p₁₊…+p_k=(q₁₊1)+…+(p_k+1)=q+k, что противоречит условию (3). Значит, граф G связный.

Пример. Деревья с числом вершин не больше 5. Приведем все попарно неизоморфные деревья с числом вершин, не больше 5: