Раздел 4
4. Понятие дискретной и цифровой линейной фильтрации аналогового сигнала.
Ранее в курсах ОТЦ и РТЦиС линейной фильтрацией называлась аналоговая линейная фильтрация (АФ), преобразующая аналоговый сигнал s1(t) в аналоговый сигнал s2(t).
Рис. 1.
При дискретной линейной фильтрации аналоговое воздействие s1(t) сначала преобразуется с помощью временного дискретизатора (ВД) в дискретный сигнал s1т(t)
Рис. 2.
Период временной дискретизации должен соответствовать требованиям Котельникова В.А., то есть
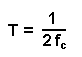
где fс – граничная частота спектра сигнала s1(t).
Непосредственно в дискретном фильтре (ДФ) осуществляются необходимые линейные операции, преобразующие дискретный сигнал s1т(t) в дискретный сигнал s2т(t), или другими словами, совокупность отсчетов {s1(nТ)} в совокупность отсчетов {s2(nТ)}.
Если
отклик фильтра требуется получить в
аналоговой форме, то после дискретной
фильтрации осуществляют преобразование
дискретного сигнала s2т(t)
в аналоговый сигнал s2(t),
то есть осуществляют восстановление
аналогового сигнала по его дискретным
отсчетам {s2(nТ)}
с помощью сглаживающего (восстанавливающего)
фильтра (СФ) – идеального фильтра НЧ,
полоса пропускания которого 2
fНЧ=2fc.
В результате сказанного структурная схема дискретной линейной фильтрации аналогового сигнала может быть изображена в виде:
Рис. 3.
При
цифровой линейной фильтрации, в отличие
от дискретной, происходит дополнительное
преобразование отсчетов воздействия
из аналоговой формы {s1(nТ)}
в цифровую
.
Величины
принимают лишь дискретные (квантованные)
значения, каждому из которых может быть
поставлено в соответствие определенное
число, в том числе, выраженное двоичным
кодом. Такое преобразование осуществляется
устройством, называемым аналого-цифровым
преобразователем (АЦП). В результате
дискретный сигнал s1т(t)
превращается в цифровой сигнал
.
Непосредственно
в цифровом фильтре (ЦФ) осуществляются
необходимые линейные операции над
совокупностью отсчетов
,
преобразующие ее в отсчеты
,
или по-другому, преобразующие цифровой
сигнал
в цифровой сигнал
.
Для
обратного преобразования цифрового
сигнала
в дискретный сигнал s2т(t)
используется устройство, называемое
цифро-аналоговым преобразователем
(ЦАП), в котором отсчеты отклика ЦФ
преобразуются из цифровой формы
в аналоговую {s2(nТ)}.
В дальнейшем, при необходимости,
дискретный сигнал s2т(t)
с помощью сглаживающего фильтра (СФ)
может быть преобразован в аналоговый
сигнал s2(t).
Исходя из сказанного, структурная схема цифровой линейной фильтрации аналогового сигнала может быть представлена в виде:
Рис. 4.
Таким образом, отличие дискретной и цифровой линейной фильтрации заключается лишь в форме представления дискретных отсчетов аналогового сигнала. Поэтому в дальнейшем анализ и синтез дискретных и цифровых линейных фильтров будем осуществлять совместно.
5.Алгоритм работы дискретного фильтра,эквивалентного аналоговому фильтру с заданной импульсной характеристикой.
Нерекурсивный дискретный фильтр.
Пусть задан аналоговый линейный фильтр, обладающий импульсной характеристикой g(t):
Рис. 5.
Алгоритм работы такого фильтра может быть представлен в виде интеграла свертки:
(1)
Для построения эквивалентного дискретного фильтра необходимо представить воздействие s1(t) и импульсную характеристику g(t) в дискретной форме, воспользовавшись разложением в ряд Котельникова В.А. Интервал дискретизации Т соответствует требованиям теоремы Котельникова В.А.
где в качестве ωc следует выбрать наибольшую из граничных частот в спектрах воздействия s1(t) и импульсной характеристики g(t). Тогда:
(2)
(3)
Подставим (2) и (3) в выражение (1) и вычислим значение отклика s2(t) в момент времени t=nT
В полученном сложном выражении под интегралом оказываются слагаемые вида:
которые содержат произведения ортогональных функций отсчетов. Так как интеграл от произведения «разноименных» ортогональных функций всегда равен нулю, то в выражении для s2(nТ) следует оставить лишь слагаемые, содержащие одноименные ортогональные функции. В нашем случае это соответствует условию: n-i=m или i=n-m.
Тогда:
В
полученном выражении постоянный
множитель
не играет принципиальной роли при
рассмотрении алгоритма вычисления
отсчета отклика s2(nТ)
и в дальнейшем может быть отброшен.
Следовательно, алгоритм работы дискретного фильтра, эквивалентного аналоговому фильтру с заданной импульсной характеристикой g(t), может быть представлен в виде:
(4)
Где |
|
- отсчеты импульсной характеристики аналогового фильтра |
Рис. 6.
Заметим,
что для реальных фильтров протяженность
функции g(t)
является конечной, поэтому число отсчетов
импульсной характеристики N
будет также конечным (
).
Следовательно, выражение (4) можно переписать в виде:
(5)
Последнее выражение представляет собой дискретный эквивалент свертки воздействия s1(t) и импульсной характеристики g(t). Как видно из выражения (5), в формировании каждого очередного отсчета отклика s2(nТ) принимает участие очередной (текущий) отсчет воздействия s1(nТ) и N его предыдущих отсчетов: s1[(n-1)T ], s1[(n-2)T ], … , s1[(n-N)T ].
Следовательно, дискретный фильтр, алгоритм которого мы получили, должен обладать памятью, в которой хранится N предыдущих отсчетов воздействия, а также содержатся (N+1) значений отсчетов импульсной характеристики аналогового фильтра {am}.
Структурная схема дискретного фильтра, реализующего алгоритм работы (5), может быть представлена в виде:
Рис. 7.
На этой схеме применены следующие обозначения:
|
- идеальный элемент задержки на время Т
- весовой умножитель с коэффициентом умножения am
- сумматор |
В принципе, структурную схему такого дискретного фильтра, названную нерекурсивным (трансверсальным), можно изобразить по-другому:
Рис. 8.
Здесь использовано обозначение:
|
- идеальный элемент задержки на время mТ |
