17. Работа при вращательном движении.

Вращательное движение тела в зависимости от времени t характеризуют угловые величины: φ (угол поворота в радианах), ω (угловая скорость в рад/сек) и ε (угловое ускорение в рад/сек2)

Закон вращательного движения тела выражается уравнением φ = f (t). Угловая скорость – величина, характеризующая быстроту вращения тела, определяется в общем случае как производная угла поворота по времени

Угловое ускорение – величина, характеризующая быстроту изменения угловой скорости, определяется как производная угловой скорости

Вращение характеризуется углом , измеряющимся в градусах или радианах, угловой скоростью (измеряется в рад/с) и угловым ускорением (единица измерения — рад/с²).

Линейная скорость точки, находящейся на расстоянии R от оси вращения

18. Кинетическая энергия вращающегося твердого тела (ось вращения неподвижна, ось вращения движется поступательно и равномерно).

Кинетическая энергия вращающегося тела есть сумма кинетических энергий его точек, т.е.

Если твердое тело движется поступательно со скоростью v и одновременно вращается с угловой скоростью ω вокруг оси, проходящей через его центр инерции, то его кинетическая энергия определяется как сумма двух составляющих:

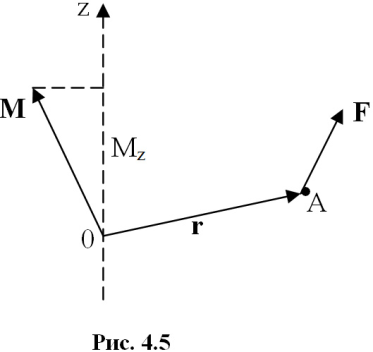
Моментом силы относительно неподвижной оси z называется скалярная величина Mz, равная проекции на эту ось вектора M момента силы, определенного относительно произвольной точки 0 данной оси. Значение момента Mz не зависит от выбора положения точки 0 на оси z.

Если ось z совпадает с направлением вектора M, то момент силы представляется в виде вектора, совпадающего с осью: Mz = |rF|z

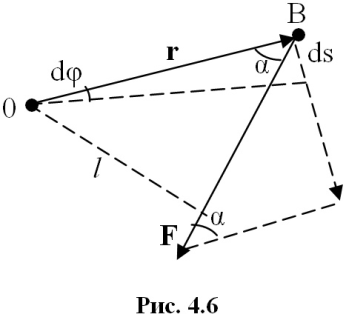
Найдем выражение для работы при вращении тела. Пусть сила F приложена к точке В, находящейся от оси вращения на расстоянии r (рис. 4.6); α – угол между направлением силы и радиусом-вектором r. Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела. При повороте тела на бесконечно малый угол dφ точка приложения В проходит путь ds = rdφ, и работа равна произведению проекции силы на направление смещения на величину смещения: dA = Fsinα*rdφ

Учитывая, что Frsinα = Mz можно записать dA = Mzdφ, где Mz - момент силы относительно оси вращения. Таким образом, работа при вращении тела равна произведению момента действующей силы на угол поворота. Работа при вращении тела идет на увеличение его кинетической энергии: dA = dEk

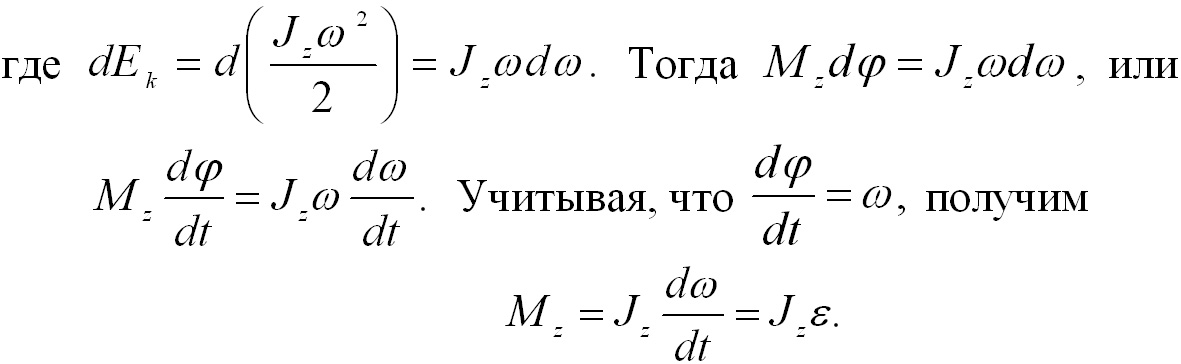
19. Элементы специальной теории относительности (постулаты сто, относительность времени, сокращение линейных размеров, релятивистская динамика).

Специальная теория относительности (СТО; также частная теория относительности) — теория, описывающая движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света. В рамках специальной теории относительности классическая механика Ньютона является приближением низких скоростей. Обобщение СТО для гравитационных полей называется общей теорией относительности.