8. Механическая энергия, ее виды. Кинетическая энергия материальной точки, системы материальных точек. Изменение кинетической энергии.

Если тело может совершить механическую работу, то оно обладает механической энергией Е (Дж). Либо, если внешняя сила совершает работу, воздействуя на тело, его энергия изменяется.

Существует два вида механической энергии: кинетическая и потенциальная.

Кинетическая энергия – энергия движущихся тел:

где v (м/с) – модуль скорости, m – масса тела.

 

Потенциальная энергия – энергия взаимодействующих тел

Примеры потенциальной энергии в механике.

Тело поднято над землей: Е = mgh

где h – высота, определяемая от нулевого уровня (или от нижней точки траектории). Форма траектории не важна, имеет значения только начальна и конечная высота.

Упруго деформированное тело. Деформация, определяемая от положения недеформированного тела (пружины, шнура и т.п.).

Кинетическая энергия механической системы — это энергия механического движения этой системы.

Сила F, действуя на покоящееся тело и вызывая его движение, совершает работу, а энергия движущегося тела возрастает на величину затраченной работы. Таким образом, работа dA силы F на пути, который тело прошло за время возрастания скорости от 0 до v, идет на увеличение кинетической энергии dT тела, т. е.

dA=dT.

Используя второй закон Ньютона

и умножая обе части равенства на перемещение dr, получим :

Так как ,то

откуда

Таким образом, тело массой m, движущееся со скоростью v, обладает кинетической энергией

Из формулы видно, что кинетическая энергия зависит только от массы и скорости тела, т. е. кинетическая энергия системы есть функция состояния ее движения.

При выводе формулы предполагалось, что движение рассматривается в инерциальной системе отсчета, так как иначе нельзя было бы использовать законы Ньютона. В разных инерциальных системах отсчета, движущихся друг относительно друга, скорость тела, а следовательно, и его кинетическая энергия будут неодинаковы. Таким образом, кинетическая энергия зависит от выбора системы отсчета.

9. Поле консервативных сил. Характеристика поля тяготения. Потенциальная энергия тела в поле тяготения. Потенциальная энергия упруго деформированных тел.

Если частица в каждой точке пространства подвержена воздействию других тел, то говорят, что эта частица находится в поле сил. Так, например, частица вблизи поверхности Земли находится в поле сил тяжести — в каждой точке пространства на нее действует сила В качестве второго примера рассмотрим заряженную частицу , находящуюся в электрическом поле, возбуждаемом неподвижным точечным зарядом q

M,

Рис. 21.1.

Рис. 21.2.

Это поле характерно тем, что направление силы, действующей на частицу в любой точке пространства, проходит через неподвижный центр (заряд ), а величина силы зависит только от расстояния до этого центра: (см. формулу (13.1)).

Поле сил, обладающее такими свойствами, называется центральным.

Если во всех точках поля силы, действующие на частицу, одинаковы по величине и направлению (F=const), поле называется однородным.

Поле, изменяющееся со временем, называется нестационарным. Поле, остающееся постоянным во времени, называют стационарным.

Для стационарного поля может оказаться, что работа, совершаемая над частицей силами поля, зависит лишь от начального и конечгного положений частицы и не зависит от пути, по которому двигалась частица. Силы, обладающие таким свойством, называются консервативными.

Из независимости работы консервативных сил от пути вытекает, что работа таких сил на замкнутом пути равна нулю. Чтобы доказать это, разобьем произвольный замкнутый путь, на две части: путь , по которому частица переходит из точки 1 в точку 2, и путь по которому тело, переходит из точки 2 в точку 1, причем точки 1 и 2 выберем произвольно (рис. 21.2). Работа на всем замкнутом пути равна сумме работ, совершаемых на каждом из участков:

Легко сообразить, что работы отличаются только знаком. Действительно, изменение направления движения на обратное приводит к замене на вследствие чего значение интеграла изменяет знак на обратный. Таким образом, равенство (21.1) можно записать в виде

и, поскольку работа не зависит от пути, т. е. , мы приходим к выводу, что А=0.

Из равенства нулю работы на замкнутом пути легко получить, что работа не зависит от пути. Это можно сделать, обратив ход проведенных выше рассуждений.

Таким образом, консервативные силы можно определить двумя способами:

1) как силы, работа которых не зависит от пути, по которому частица переходит из одного положения в другое;

2) как силы, работа которых на любом замкнутом пути равна нулю.

По́ле тяготе́ния — физическое поле, через которое осуществляется гравитационное взаимодействие.

Потенциальная энергия - механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.

Пусть взаимодействие тел осуществляется посредством силовых полей (например, поля упругих сил, поля гравитационных сил), характеризующихся тем, что работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений. Такие поля называются потенциальными, а силы, действующие в них,— консервативными. Если

же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипативной; ее примером является сила трения.

Рассмотрим, чему равна работа, совершаемая силами поля тяготения при перемещении в нем материальной точки массой m. Вычислим, например, какую надо затратить работу для удаления тела массой т от Земли. На расстоянии R на данное тело действует сила

F=GmM/R².

При перемещении этого тела на расстояние dR затрачивается работа

Знак минус появляется потому, что сила и перемещение в данном случае противоположны по направлению .

Если тело перемещать с расстояния R₁ до R₂, то затрачивается работа

Из формулы вытекает, что затраченная работа в иоле тяготения не зависит от траектории перемещения, а определяется лишь начальным и конечным положениями тела, т. е. силы тяготения действительно консервативны, а поле тяготения является потенциальным.

F =mG

Вектор g не зависит от m и называется напряженностью поля тяготения. Напряженность поля тяготения определяется силой, действующей со стороны поля на материальную точку единичной массы, и совпадает по направлению с действующей силой. Напряженность есть силовая характеристика поля тяготения.

Найдем потенциальную энергию упругодеформированного тела (пружины). Сила упругости пропорциональна деформации: F_xупр= - kx

где F_xynp — проекция силы упругости на ось х; k — коэффициент упругости (для пружины — жесткость), а знак минус указывает, что Fупр направлена в сторону, противоположную деформации х.

По третьему закону Ньютона, деформирующая сила равна по модулю силе упругости и противоположно ей направлена, т. е. F_x= -F_хупр=kx

Элементарная работа dA, совершаемая

силой Fx при бесконечно малой деформации dх, равна

а полная работа

идет на увеличение потенциальной энергии пружины. Таким образом, потенциальная

энергия упругодеформированного тела Потенциальная энергия системы, подобно кинетической энергии, является функцией состояния системы. Она зависит только от конфигурации системы и ее положения по отношению к внешним телам.

10. Закон сохранения механической энергии, его связь с однородностью времени.

Идея этого закона принадлежит М.В. Ломоносову,изложившему закон сохранения материи и движения,а количественная формулировка закона сохранения энергии дана Ю. Майером и Г. Гельмгольцем.

Механическя энергия консервативной системы с течением времени не изменяется

Энергия потенциальная +энергия кинетическая = константа

ЗСМЭ связан с однородностью времени ,которая проявляется в том что законы движущие замкнутой системой не зависят от выбора начала системы отсчета времени.

11. Кинематика вращательного движения: вектор элементарного угла поворота, угловая скорость, угловое ускорение. Связь угловых и линейных характеристик при вращательном движении.

точки твердого тела вращаюшегося вокруг неподвижной оси,движушегося по окружностям центры которых лежат на оси вращения

За dt радиус вектор r повернется на угол dфи ,его направление связано с направлением вращ. ,правилом правого винта.

Dфи(с вектором)-максимальный угол элементарного поворота

Dфи(без вектора)-модуль вектора элементарного угла поворота

Угловая скорость-векторная величина равная производной вектора элементарного угла поворота по времени(w) совпадает по направлению с dфи(векторная величина)

При равномерном вращении:

Связь линейной и угловой скорости:

-векторное произведение

Учтено:(

Угловое ускорение-векторная величина равная производной вектора угловой скорости по времени

если>0 то укоренное если <0 то замедленное

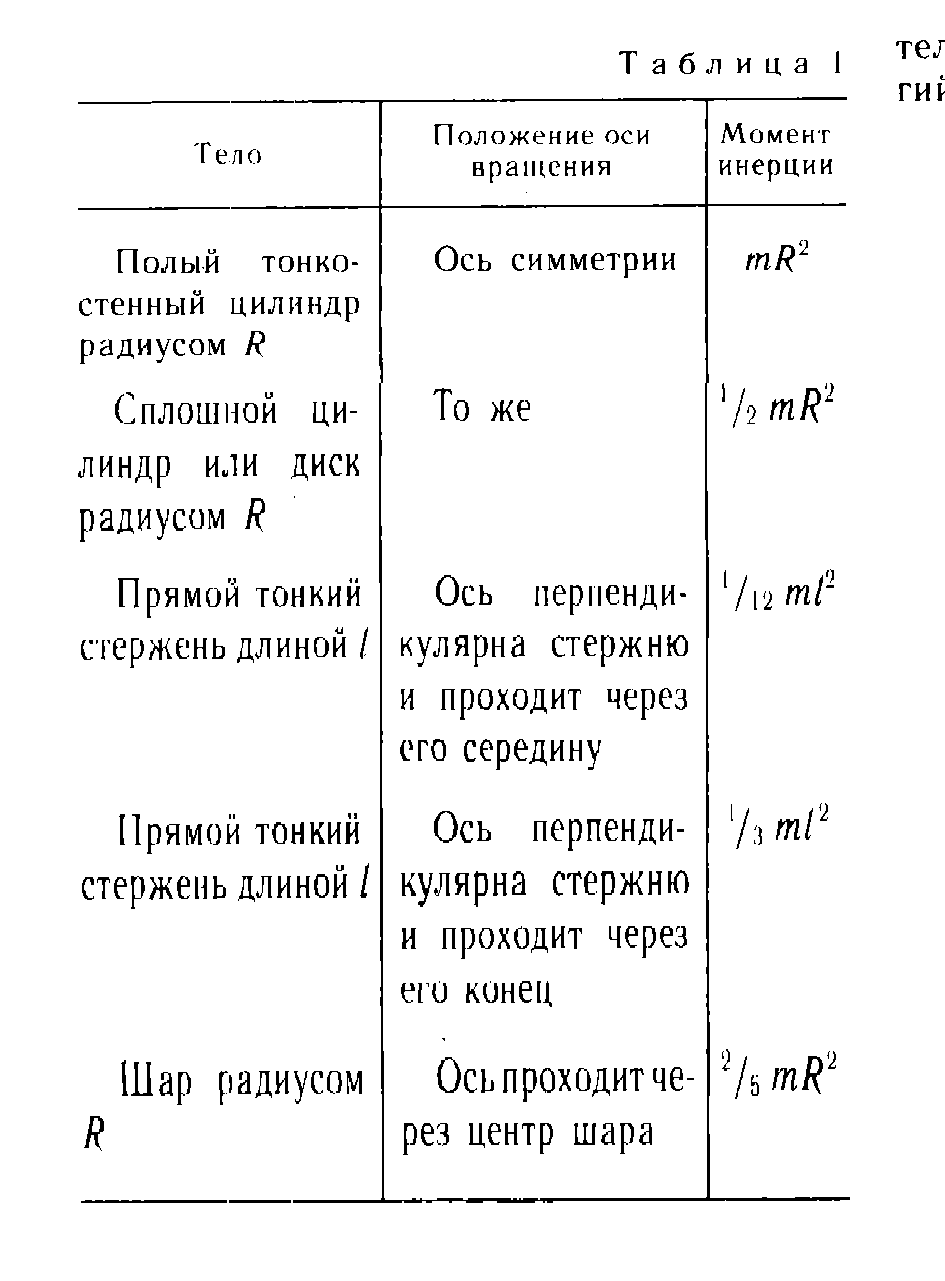
12. Момент инерции (материальной точки, системы материальных точек, твердого тела). Моменты инерции тел правильной геометрической формы относительно оси, проходящей через центр масс. Теорема Штейнера.

момент инерции характеризует инертные свойства тел пр вращательном движении

-момент инерции МТ относительно неподвижной оси Z

-момент инерции системы МТ относительно оси Z

-момент инерции твердого тела относитеьно неподвижной оси Z

13. Момент силы (относительно неподвижной точки, относительно неподвижной оси).

Моментом силы F относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора г, проведенного из точки О в точку А приложения силы, на силу F.

Здесь М — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от г к F.

Модуль момента силы

M = Fr sin a = Fl где а — угол между г и F; r sina = l — кратчайшее расстояние между линией действия силы и точкой О — плечо силы.

Моментом силы относительно неподвижной оси z называется скалярная величина М2, равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки О данной оси z. Значение момента Мz не зависит от выбора положения точки О на оси z.

Eсли ось z совпадает с направлением вектора М, то момент силы представляется в виде вектора, совпадающего с осью:

Mz= [rF]_z.