Работа силы упругости

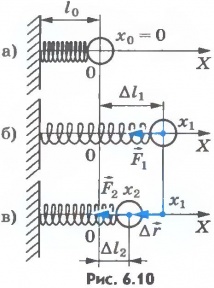
На рисунке 6.10, а показана пружина, у которой один конец закреплен неподвижно, а к другому концу прикреплен шар. Если пружина растянута, то она действует на шар с силой  (рис.6.10,б), направленной к положению равновесия шара, в котором пружина не деформирована. Начальное удлинение пружины равно . Вычислим работу силы упругости при перемещении шара из точки с координатой x₁ в точку с координатой x₂. Из рисунка 6.10, в видно, что модуль перемещения равен:

где - конечное удлинение пружины.

   Вычислить работу силы упругости по формуле (6.2) нельзя, так как эта формула справедлива лишь для постоянной силы, а сила упругости при изменении деформации пружины не остается постоянной. Для вычисления работы силы упругости воспользуемся графиком за¬висимости модуля силы упругости от координаты шара (рис.6.11).

   В § 43 мы показали, что при постоянном значении проекции силы на перемещение точки приложения силы ее работа может быть определена по графику зависимости F_x от x и что эта работа численно равна площади прямоугольника. При произвольной зависимости F_x от x, разбивая перемещение на малые отрезки, в пределах каждого из которых силу можно считать постоянной, увидим, что работа будет численно равна площади трапеции.    В нашем примере работа силы упругости на перемещении точки ее приложения  численно равна площади трапеции ВCDM. Следовательно,

   Согласно закону Гука и . Подставляя эти выражения для сил в уравнение (6.17) и учитывая, что , получим

Или окончательно

   Мы рассмотрели случай, когда направления силы упругости и перемещения тела совпадали: . Но можно было бы найти работу силы упругости, когда ее направление противоположно перемещению тела или составляет с ним произвольный угол, а также при перемещении тела вдоль кривой произвольной формы.    Во всех этих случаях движения тела под действием силы упругости мы пришли бы к той же формуле для работы (6.18). Работа сил упругости зависит лишь от деформаций пружины и  в начальном и конечном состояниях.    Таким образом, работа силы упругости не зависит от формы траектории и, так же как и сила тяжести, сила упругости является консервативной.

В физике консервативные си́лы (потенциальные силы) — это силы, работа которых не зависит от вида траектории, точки приложения этих сил и закона их движения и определяется только начальным и конечным положением этой точки^[1]. Равносильным определением является и следующее: консервативные силы — это такие силы, работа которых по любой замкнутой траектории равна 0.

Силы, работа которых на замкнутом пути не равна нулю, называются неконсервативными. К числу таких сил относятся, например, сила трения и сила вязкого сопротивления. Легко понять, что при движении частицы по замкнутому контуру работа подобных сил будет отрицательной.

В теоретической физике выделяют только четыре типа сил, каждая из которых является консервативной (см. Фундаментальные взаимодействия). В школьной программе по физике силы разделяют на консервативные и неконсервативные. Примерами консервативных сил являются: сила тяжести, сила упругости, сила кулоновского (электростатического) взаимодействия. Примером неконсервативной силы является сила трения.

Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется.

Для консервативных сил выполняются следующие равенства:

— работа, производимая консервативной силой, определяется только начальным и конечным положением точки её приложения и не зависит от выбора траектории, по которой перемещается тело.

 — работа консервативных сил по произвольному замкнутому контуру равна 0;

 — ротор консервативных сил равен 0;

 — консервативная сила является градиентом некой скалярной функции , называемой силовой. Эта функция равна потенциальной энергии взятой с обратным знаком. Соответственно, и связаны соотношением

Таким образом, потенциальная сила всегда направлена в сторону уменьшения потенциальной энергии.

Мо́щность — физическая величина, равная в общем случае скорости изменения, преобразования, передачи или потребления энергии системы. В более узком смысле мощность равна отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени^[1].

Различают среднюю мощность за промежуток времени

и мгновенную мощность в данный момент времени:

Интеграл от мгновенной мощности за промежуток времени равен полной переданной энергии за это время:

Если на движущееся тело действует сила, то эта сила совершает работу. Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:

где F — сила, v — скорость,  — угол между вектором скорости и силы.

Частный случай мощности при вращательном движении:

M — момент силы,  — угловая скорость,  — число пи, n — частота вращения (число оборотов в минуту, об/мин.)