6. Закон сохранения импульса, его связь с однородностью пространства.

Зако́нсохране́нияи́мпульса (Зако́нсохране́ния количества движения) утверждает, что векторная сумма импульсов всех тел (или частиц) системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему, равна нулю.

В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил.

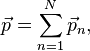
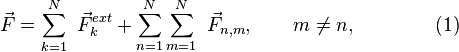
Здесь   — равнодействующая сил, действующим на n-ю частицу со стороны m-ой, а   — равнодействующая всех внешних сил, действующих k-ю частицу. Согласнотретьему закону Ньютона, силы вида   и   будут равны по абсолютному значению и противоположны по направлению, то есть  . Поэтому вторая сумма в правой части выражения (1) будет равна нулю

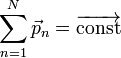
7. Механическая работа. Работа силы тяготения и силы упругости. Консервативные и неконсервативные силы. Мощность.

Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек), тела или системы.

Если тело под действием силы  совершает перемещение , работа А этой силы равна скалярному произведению силы на вектор перемещения. Работа силы есть скалярная величина

A=

A=

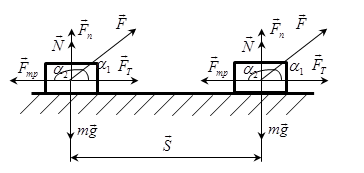
   Работа горизонтальной составляющей силы F - силы F_тяги равна ( )

  

Работа вертикальной составляющей силы F - силы подъёма F_n равна ( )

Сила, направление которой перпендикулярно направлению движению тела, работу не совершает. Работа силы трения равна ( ).

Работа

Работа силы тяжести

Сила тяжести равна F = mg и направлена по вертикали вниз. Вблизи поверхности Земли ее можно считать постоянной. При движении тела по вертикали вниз сила тяжести совпадает по направлению с перемещением. При переходе с высоты h₁ над каким-то уровнем, от которого мы начинаем отсчет высоты, до высоты h₂ над тем же уровнем (рис. 192), тело совершает перемещение, по абсолютной величине равное h₁ - h₂.

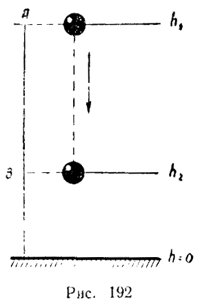
Так как направления перемещения и силы совпадают, то работа силы тяжести положительна и равна:

Высоты h₁ и h₂ не обязательно отсчитывать от поверхности Земли. Для начала отсчета высот можно выбрать любой уровень. Это может быть пол комнаты, стол или стул, это может быть и дно ямы, вырытой в земле, и т. д. Ведь в формулу для работы входит разность высот, а она не зависит от того, откуда начинать их отсчет. Мы могли бы, например, условиться начинать отсчет высоты с уровня В (см. рис. 192). Тогда высота этого уровня была бы равна нулю, а работа выражалась бы равенством

где h — высота точки A над уровнем В.

Если тело движется вертикально вверх, то сила тяжести направлена против движения тела и ее работа отрицательна. При подъеме тела на высоту h над тем уровнем, с которого оно брошено, сила тяжести совершает работу, равную

Если после подъема вверх тело возвращается в исходную течку, то работа на таком пути, начинающемся и кончающемся в одной и той же точке (на замкнутом пути), на пути «туда и обратно», равна нулю. Это одна из особенностей силы тяжести: работа силы тяжести на замкнутом пути равна нулю. Теперь выясним, какую работу совершает сила тяжести в случае, когда тело движется не по вертикали. В качестве примера рассмотрим движение тела по наклонной плоскости (рис. 193).

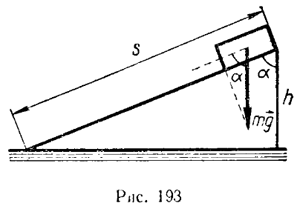
Допустим, что тело массой m по наклонной плоскости высотой h совершает перемещение s, по абсолютной величине равное длине наклонной плоскости. Работу силы тяжести mg в этом случае надо вычислять по формуле

Но из рисунка видно, что

Поэтому

Мы получили для работы то же самое значение. Выходит, что работа силы тяжести не зависит от того, движется ли тело по вертикали или проходит более длинный путь по наклонной плоскости. При одной и той же «потере высоты» работа силы тяжести одинакова (рис. 194).

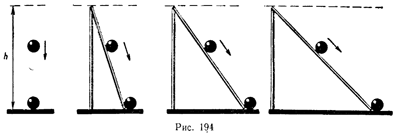
Это справедливо не только при движении по наклонной плоскости, но и по любому другому пути. В самом деле, допустим, что тело движется по какому-то произвольному пути, например по такому, какой изображен на рисунке 195.

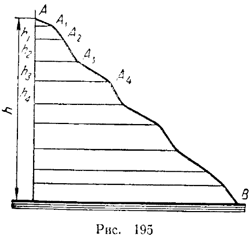
Весь этот путь мы можем мысленно разбить на ряд малых участков: AA₁, A₂A₁, A₂A₃ и т. д. Каждый из них может считаться маленькой наклонной плоскостью, а все движение тела на пути АВ можно представить как движение по множеству наклонных плоскостей, переходящих одна в другую. Работа силы тяжести на каждой такой наклонной плоскости равна произведению mg на изменение высоты тела на ней. Если изменения высот на отдельных участках равны h₁, h₂, h₃ и т. д., то работы силы тяжести на них равны mgh₁, mgh₂, mgh₃ и т. д. Тогда полную работу на всем пути можно найти, сложив все эти работы:

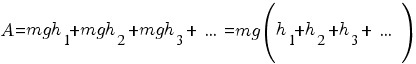
Ho

Следовательно,

Таким образом, работа силы тяжести не зависит от траектории движения тела и всегда равна произведению силы тяжести на разность высот в исходном и конечном положениях. При движении вниз работа положительна, при движении вверх — отрицательна. Почему же в технике и быту при подъеме грузов часто пользуются наклонной плоскостью? Ведь работа перемещения груза по наклонной плоскости такая же, как и при движении по вертикали! Это объясняется тем, что при равномерном движении груза по наклонной плоскости сила, которая должна быть приложена к грузу в направлении перемещения, меньше силы тяжести. Правда, груз при этом проходит больший путь. Больший путь — это плата за то, что по наклонной плоскости груз можно поднимать с помощью меньшей силы.