15. Расчет разности потенциалов двух точек электростатического поля:

а) поле точечного заряда, равномерно заряженной сферической поверхности;

б) поле равномерно заряженной бесконечной плоскости;

в) поле равномерно заряженной длинной нити (цилиндра).

• Поле точечного заряда, равномерно заряженной сферической поверхности

напряженность поля сферы определяется формулой : (рис. 3.11 ). А т.к. , то

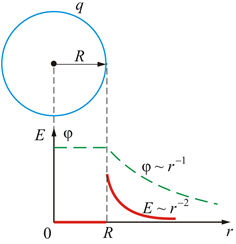
(рис.3.11)

.

Если принять r1=r , а r2=∞, то потенциал вне сферической поверхности определяется выражением Внутри сферической поверхности потенциал всюду одинаков и равен , так как напряженность поля внутри сферической поверхности равна нулю.

Отсюда имеем

• Поле равномерно заряженной бесконечной плоскости

Поле равномерно заряженной бесконечной плоскости, найденная с помощью теоремы Остроградского-Гаусса, определяется по формуле , где σ – поверхностная плотность заряда. Разность потенциалов между точками, лежащими на расстояниях x₁иx₂ от плоскости, равна .

• Поле равномерно заряженной длинной нити (цилиндра)

С помощью теоремы Остроградского-Гаусса мы показали, что, т.к. , то (рис. 3.9 )

(33)

где – линейная плотность заряда.

Тогда, т.к. , отсюда следует разность потенциалов в произвольных точках 1 и 2 будет равна:

.

(34)

На рисунке 3.6 изображена зависимость напряженности E и потенциала от r. (Здесь и далее E – изображена сплошной линией, а – пунктирной).

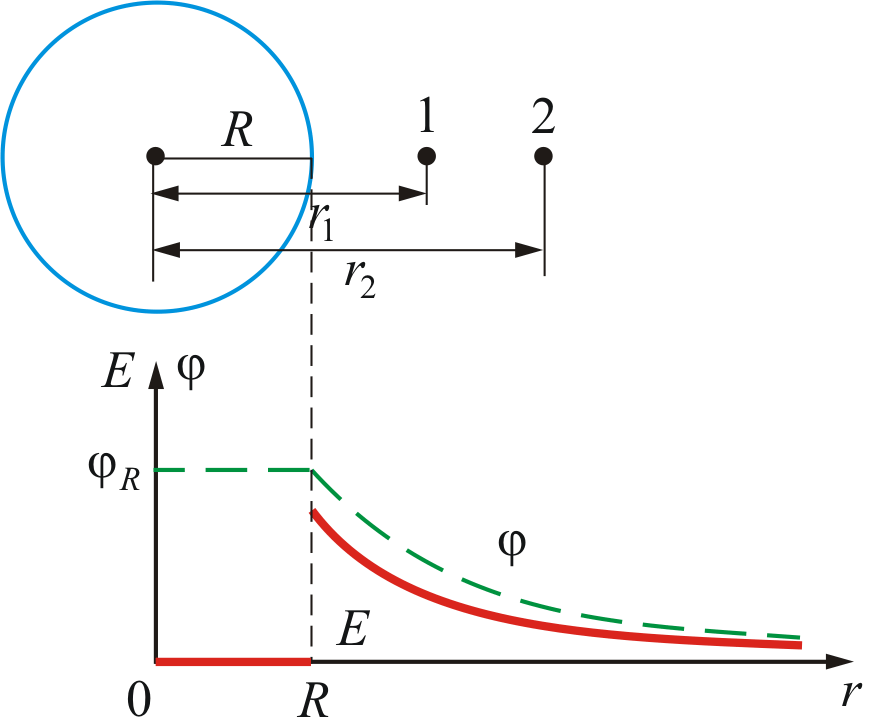
Рисунок 3.9

16. Электрический диполь. Полярные, неполярные и ионные диэлектрики. Сегнетоэлектрики.

Э лектрическим диполем называется совокупность двух равных зарядов противоположного знака, находящихся друг от друга на расстоянии l, малом по сравнению с их расстоянием до точек, в которых определяется поле диполя.

Произведение заряда на расстояние между зарядами р=qlназывается дипольным моментом. Для полного определения диполя нужно задать еще и ориентацию оси диполя в пространстве. В соответствии с этим дипольный момент следует рассматривать как вектор . Этому вектору приписывают направление от отрицательного заряда к положительному (рис.3.3). Если ввести радиус – вектор проведенный от –q к +q, то дипольный момент можно представить в виде:

Полярные диэлектрики (дипольные) — состоят из полярных молекул, обладающих электрическим моментом. В таких молекулах из-за их асимметричного строения центры масс положительных и отрицательных зарядов не совпадают. При замещении в неполярных полимерах некоторой части водородных атомов другими атомами или не углеводородными радикалами получаются полярные вещества. При определении полярности вещества по химической формуле следует учитывать пространственное строение молекул. К полярным диэлектрикам относятся феноло-формальдегидные и эпоксидные смолы, кремнийорганические соединения, хлорированные углеводороды и др.

Неполярные диэлектрики (нейтральные) — состоят из неполярных молекул, у которых центры тяжести положительного и отрицательного зарядов совпадают. Следовательно неполярные молекулы не обладают электрическим моментом и их электрический момент p = q • l = 0. Примером практически неполярных диэлектриков, применяемых в качестве электроизоляционных материалов, являются углеводороды, нефтяные электроизоляционные масла, полиэтилен, полистирол и др.

Примеры молекул неполярных и полярных веществ

Ионные соединения представляют собой твердые неорганические диэлектрики с ионным типом химической связи. Для этой группы соединений характерны, кроме электронной, ионная и электронно-релаксационная поляризации. Принято выделять группу диэлектриков с быстрыми видами поляризаций — электронной и ионной, и с замедленными видами поляризаций релаксационного типа, накладывающихся на электронную и ионную поляризацию. К первой группе, в которой наблюдаются только быстрые виды поляризаций, относятся кристаллические вещества с плотной упаковкой ионов. К ним относятся каменная соль, кварц, слюда, корунд, двуокись титана (рутил) и др. Ко второй группе, в которой кристаллические диэлектрики с неплотной упаковкой частиц в решетке имеют также и ионно - релаксационную поляризацию, относятся неорганические стекла, электротехнический фарфор, ситаллы, микалекс и др.

Сегнетоэлектрики, кристаллические диэлектрики, обладающие в определённом интервале температур спонтанной (самопроизвольной) поляризацией, которая существенно изменяется под влиянием внешних воздействий. Электрические свойства С. во многом подобны магнитным свойствам ферромагнетиков (отсюда название ферроэлектрики, принятое в зарубежной литературе). К числу наиболее исследованных и используемых на практике С. относятся титанат бария, сегнетова соль (давшая название всей группе кристаллов), триглицинсульфат, дигидрофосфат калия и др.