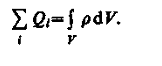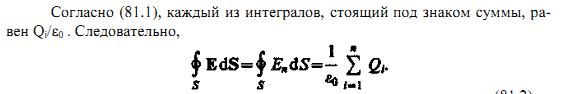- •Основные понятия кинематики: система отсчета, относительность движения и покоя, радиус-вектор, вектор перемещения, пройденный путь, кинематические уравнения движения .
- •Относительность Движения и покоя :
- •Кинематические уравнения движения :
- •Скорость (вектор средней скорости, средняя скорость неравномерного движения, скорость в данный момент времени). Проекция вектора скорости на координатные оси.
- •Ускорение (среднее и мгновенное). Проекция вектора ускорения на координатные оси, проекция вектора ускорения на направление касательной к траектории и на направление нормали к касательной.
- •Инерциальные системы отсчета. Взаимодействия и силы. Силы в механике: гравитационная, упругости, трения. Уравнение динамики материальной точки, системы материальных точек.
- •Импульс, его изменение. Центр масс механической системы, закон движения центра масс.
- •Закон сохранения импульса, его связь с однородностью пространства.
- •Механическая работа. Работа силы тяготения и силы упругости. Консервативные и неконсервативные силы. Мощность.
- •Работа силы тяжести
- •Работа силы упругости
- •Механическая энергия, ее виды. Кинетическая энергия материальной точки, системы материальных точек. Изменение кинетической энергии.
- •Поле консервативных сил. Характеристика поля тяготения. Потенциальная энергия тела в поле тяготения. Потенциальная энергия упруго деформированных тел.
- •Момент импульса материальной точки и системы материальных точек (относительно неподвижной точки, относительно неподвижной оси).
- •Работа при вращательном движении.
- •Кинетическая энергия вращающегося твердого тела (ось вращения неподвижна, ось вращения движется поступательно и равномерно).
- •Элементы специальной теории относительности (постулаты сто, относительность времени, сокращение линейных размеров, релятивистская динамика).
- •Постулаты сто
- •Относительность времени
- •Сокращение линейных размеров
- •Термодинамические системы, статистический и термодинамический методы их исследования, Макроскопические и микроскопические параметры системы.
- •Уравнение Клапейрона - Менделеева. Основное уравнение молекулярно-кинетической теории идеальных газов. Средняя энергия теплового движения молекул.
- •Распределение молекул по скоростям теплового движения (распределение Максвелла). Закон равномерного распределения энергии по степеням свободы. Внутренняя энергия идеального газа.
- •Количество теплоты. Первое начало термодинамики. Теплоемкость, ее зависимость от типа процесса. Адиабатный процесс.
- •Теплоемкость.
- •Энтропия. Изменение энтропии при различных процессах. Закон возрастания энтропии. Второе начало термодинамики.
- •Изменение энтропии в изопроцессах
- •Круговые процессы. Тепловые двигатели и холодильные машины. Кпд тепловой машины. Цикл Карно, кпд цикла Карно.
- •Круговой процесс (цикл). Обратимые и необратимые процессы.
- •Тепловые двигатели и холодильные машины. Цикл Карно и его к. П. Д. Для идеального газа
- •Средняя длина свободного пробега молекул, среднее число их столкновений в единицу времени.
- •. Средняя длина свободного пробега молекул.
- •Потенциал электростатического поля — скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду:
- •Расчет напряженности электростатического поля, созданного:
- •Работа кулоновских сил по перемещению заряда. Напряженность как градиент потенциала. Эквипотенциальные поверхности.
- •Расчет разности потенциалов двух точек электростатического поля:
- •Электрический диполь. Полярные, неполярные и ионные диэлектрики. Сегнетоэлектрики.
- •Поляризация диэлектриков (деформационная, ориентационная, ионная).
- •Поляризованность (вектор поляризации).
- •Электростатическое поле в диэлектрике. Диэлектрическая восприимчивость. Диэлектрическая проницаемость.
- •Проводники в электростатическом поле. Электростатическая индукция.
- •Электроемкость уединенного проводника. Электроемкость конденсатора.
- •Электроемкость уединенного проводника
- •Энергия уединенного заряженного проводника:
- •Энергия заряженного конденсатора. Энергия электростатического поля.
- •Энергия электростатического поля.
- •Электрический ток, его характеристики: сила и плотность тока.
- •Неоднородный участок электрической цепи. Закон Ома в интегральной и дифференциальной (локальной) форме записи для неоднородного участка электрической цепи.
- •Закон Джоуля – Ленца для однородного участка электрической цепи в интегральной и дифференциальной (локальной) форме записи.
- •Магнитное поле, его характеристики.
- •Закон Био - Савара – Лапласа, его применение для расчета индукции магнитного поля, созданного:
- •Закон полного тока (теорема о циркуляции вектора индукции магнитного поля), его применение для расчета индукции поля длинного соленоида.
- •Применение закона для расчета индукции поля длинного соленоида
- •Силы в магнитном поле (сила Ампера, сила Лоренца).
- •Поток вектора индукции магнитного поля. Теорема Гаусса для вектора индукции магнитного поля.
Потенциал электростатического поля — скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду:
Принцип
суперпозиции электростатических полей
- напряженность Е результирующего
по-ля, создаваемого системой зарядов,
равна геометрической сумме напряженно-стей
полей, создаваемых в данной точке каждым
из зарядов в отдельности. E=

Поток вектора напряженности электростатического поля. Теорема Гаусса для электростатического поля в вакууме.
Согласно принципу суперпозиции, напряженность Е поля диполя в произвольной точке
![]() где Е+ и Е_ —
напряженности полей, создаваемых
соответственно положительным и
отрицательным зарядами. Воспользовавшись
этой формулой, рассчитаем напряженность
поля в произвольной точке на продолжении
оси диполя и на перпендикуляре к середине
его оси.
где Е+ и Е_ —
напряженности полей, создаваемых
соответственно положительным и
отрицательным зарядами. Воспользовавшись
этой формулой, рассчитаем напряженность
поля в произвольной точке на продолжении
оси диполя и на перпендикуляре к середине
его оси.
Напряженность поля на продолжении оси диполя в точке А (рис. 123).
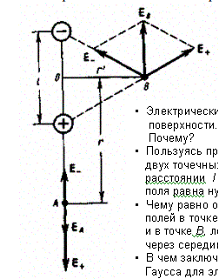
Как видно из рисунка, напряженность поля диполя в точке А направлена по оси
д иполя
и по модулю равна
иполя
и по модулю равна ![]()

Теорема Гаусса для электростатического поля в вакууме.
Вычисление напряженности поля системы электрических зарядов с помощью принципа суперпозиции электростатических полей можно значительно упростить, используя выведенную немецким ученым К. Гауссом (1777—1855) теорему, определяющую поток вектора напряженности электрического поля сквозь произвольную замкнутую поверхность. В соответствии с формулой (79.3) поток вектора напряженности сквозь сферическую поверхность радиуса r, охватывающую точечный заряд Q, находящийся в ее центре (рис. 124), равен
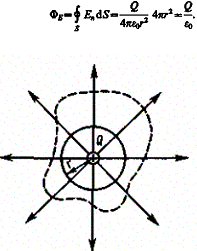
Этот результат справедлив для замкнутой поверхности любой формы. Действительно, если окружить сферу (рис. 124) произвольной замкнутой поверхностью, то каждая линия напряженности, пронизывающая сферу, пройдет и сквозь эту поверхность. Если замкнутая поверхность произвольной формы охватывает заряд то при пересечении любой выбранной линии напряженности с поверхностью она то входит в нее, то выходит из нее.
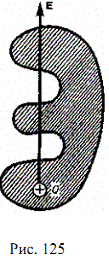
Нечетное число пересечений при вычислении потока в конечном счете сводится к одному пересечению, так как поток считается положительным, если линии напряженности выходят из поверхности, и отрицательным для линий, входящих в поверхность. Бели замкнутая поверхность не охватывает заряда, то поток сквозь нее равен нулю, так как число линий напряженности, входящих в поверхность, равно числу линий напряженности, выходящих из нее. Таким образом, для поверхности любой формы, если она замкнута и заключает в себя точечный заряд Q, поток вектора Е будет равен Q/0, т. е.
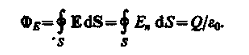
Знак
потока совпадает со знаком заряда Q.
Рассмотрим общий случай произвольной
поверхности, окружающей n зарядов. В
соответствии с принципом суперпозиции
(80.2) напряженность Е поля, создаваемого
всеми зарядами, равна сумме напряженностей
Е, полей, создаваемых каждым зарядом в
отдельности:
![]()
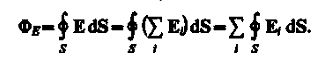

Формула
(81.2) выражает теорему Гаусса для
электростатического поля в вакууме:
поток вектора напряженности
электростатического поля в вакууме
сквозь произвольную замкнутую поверхность
равен алгебраической сумме заключенных
внутри этой поверхности зарядов, деленной
на 0. Эта теорема выведена математически
для векторного поля любой природы
русским математиком М. В. Остроградским
(1801—1862), а затем независимо от него
применительно к электростатическому
полю — К. Гауссом. В общем случае
электрические заряды могут быть
«размазаны» с некоторой объемной
плотностью p = dQ/dV, различной в разных
местах пространства. Тогда суммарный
заряд, заключенный внутри замкнутой
поверхности S, охватывающей некоторый
объем V,