МЕХАНИКА

1. Основные понятия кинематики: система отсчета, относительность движения и покоя, радиус-вектор, вектор перемещения, пройденный путь, кинематические уравнения движения .

система отсчета — совокупность системы координат и часов, связанных с телом отсчета.

Относительность Движения и покоя :

Всякое движение, а также покой тела (как частный случай движения) относительны. Отвечая на вопрос, покоится тело или движется и как именно движется, необходимо указать, относительно каких тел рассматривается движение данного тела. Иначе никакое высказывание о его движении не может иметь смысла.

Тела, относительно которых рассматривается данное движение, называют системой отсчета. Выбор системы отсчета при изучении данного движения делают в зависимости от условий задачи. Так, чтобы попасть во вражеский самолет с земной поверхности, нужно установить придел, исходя из скорости самолета в системе отсчета «Земля» (в нашем примере — 800 км/ч), а чтобы попасть в этот же самолет со встречного самолета, надо исходить из скорости цели в системе отсчета «встречный самолет» (1600 км/ч). При изучении движений на поверхности Земли обычно принимают за систему отсчета Землю (хотя, как сказано, можно выбрать за систему отсчета и поезд, и самолет, и любое другое тело). Изучая движение Земли в целом или движение планет, принимают за систему отсчета Солнце и звезды. Как увидим в гл. II, эта система особенно удобна при изучении законов динамики.

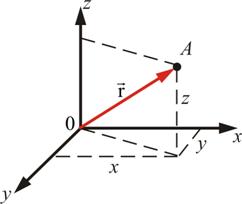
Ра́диус-ве́ктор (обычно обозначается или просто ) — вектор, задающий положения точки в пространстве (например, гильбертовом или векторном) относительно некоторой заранее фиксированной точки, называемой началом координат.

Перемеще́ние (в кинематике) — изменение местоположения физического тела в пространстве относительно выбранной системы отсчёта. Также перемещением называют вектор, характеризующий это изменение . Можно определить перемещение, как изменение радиус-вектора точки: .

Модуль перемещения совпадает с пройденным путём в том и только в том случае, если при движении направление скорости не изменяется. При этом траекторией будет отрезок прямой. В любом другом случае, например, при криволинейном движении, из неравенства треугольника следует, что путь строго больше.

Мгновенная скорость точки определяется как предел отношения перемещения к малому промежутку времени, за которое оно совершено. Более строго:

.

Путь- расстояние, которое прошло тело по траектории. Пройденный путь - Число единиц длины, пройденных точкой с начала движения.

Кинематические уравнения движения :

В координатном виде : х=х(t) : y=y(t) ; z=z(t)

В векторном oно эквивалентно трем координатным уравнениям. Координатные и векторные уравнения движения связаны между собой, т.к. радиус–вектор можно представить в виде Модуль радиус–вектора равен 

2. Скорость (вектор средней скорости, средняя скорость неравномерного движения, скорость в данный момент времени). Проекция вектора скорости на координатные оси.

Скорость – физическая величина, показывающая , какое перемещение совершило тело за единицу времени.

Вектор средней скорости называется отношение приращения ∆ r радиуса вектора точки к промежутку времени ∆t .

При неограниченном уменьшении ∆ r средняя скорость стремится к предельному значению, которое называется мгновенной скоростью v:

Мгновенная скорость v, таким образом, есть векторная величина, равная первой производной радиуса-вектора движущейся точки по времени. Так как секущая в пределе совпадает с касательной, то вектор скорости v направлен по касательной к траектории в сторону движения . По мере уменьшения ∆t путь ∆s все больше будет приближаться к |∆г|, поэтому модуль мгновенной скорости

При неравномерном движении модуль мгновенной скорости с течением времени изменяется. В данном случае пользуются скалярной величиной —средней скоростью неравномерного движения: