36. Формулировка и доказательство теоремы Лагранжа.

Пусть:

1. Функция   непрерывна на отрезке  :  ;

2. Функция дифференцируема на интервале  : 

.

Тогда существует такая точка  , что  .

Доказательство

Рассмотрим вспомогательную функцию  .

1. Эта функция непрерывна, т.к.  ,  - непрерывна.

2. Данная функция имеет производную  , так как для любого  .

3. Значения на концах равны:  ,  .

Эти 3 рассуждения удовлетворяют условию теоремы Ролля, следовательно,  . Таким образом,  ,  .

Формулировки теоремы:

1. Обозначая  , где  .  ;

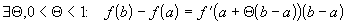2. Обозначая  , получаем  , или  . Обозначая также  , получаем  , где также  .

(Первое следствие теоремы Лагранжа)

(Критерий постоянства функции на промежутке).

Пусть существует множество  , и для всякого   значение производной равно 0. Тогда данная функция является постоянной, т.е.  .

Доказательство

. Очевидно, что  .

. Достаточно доказать, что  . Ранее доказано (14.2), что из дифференцируемости функции в точке следует ее непрерывность. Поэтому  , и, в частности,  . Так как   и  . Значит, по теореме Лагранжа,   такое, что  , т.к.  . Следовательно,  .

Данное следствие часто называется основной леммой интегрального исчисления.

Замечание

Если X состоит из нескольких отрезков, то функция будет постоянной на каждом из этих отрезков, но эти постоянные могут быть не равны.

Второе следствие теоремы Лагранжа

Если для любого   значение производной больше 0, то эта функция возрастает на интервале  . (Если меньше 0 - убывает).

Доказательство

Пусть существуют   такие, что  . Функция   непрерывна на отрезке  , так как она дифференцируема на   и  . Тогда  , т.е. дифференцируема и на  . Значит, по теореме Лагранжа,  . Так как всегда  , то значение   непосредственно зависит от значения производной. То есть знак функции совпадает со знаком производной.

Третье следствие теоремы Лагранжа)

Пусть X - некоторый промежуток, и значения производной на этом промежутке ограничены числом C:  . Тогда функция   равномерно непрерывна на данном промежутке.

Доказательство

Требуется доказать, что   (см. определение равномерной непрерывности - п. 13). По теореме Лагранжа имеем:  . Обозначив  , получаем:  . 

Пример: функция  , имеющая ограниченную производную  , . Данная функция действительно является равномерно непрерывной. 37. Теорема Коши

Пусть функции y = f(x), y = g(x) непрерывны на отрезке и дифференцируемы на интервале (a, b), причем g ' (x) ≠ 0 на (a, b).

Тогда существует число c (a,b) такое, что 

Доказательство

Заметим, что g(b) ≠ g(a). (Если g(b) = g(a), то, по теореме Ролля, существует число c (a,b)такое, что g ' (c) = 0.)

Введем обозначение:  .

Рассмотрим функцию  , которая непре-рывна на [a,b], дифференцируема на (a, b) и F(a) = F(b) = 0, т.е. функция F удовлетворяет условиям теоремы Ролля.

Следовательно, существует число c (a,b) такое, что F ' (c) = 0.

Так как 

Теорема доказана

38. Формула Тейлора с остаточным членом в форме Лагранжа.

     Формула Тейлора 

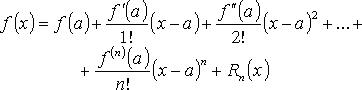
(R_n(x) - остаточный член формулы Тейлора).

     Остаточный член формулы Тейлора 

     В форме Лагранжа:

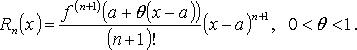
39. Правило Лопиталя и его применения к раскрытию неопределенностей при вычислении пределов Дифференциальное исчисление значительно облегчает задачу раскрытия неопределенностей при вычислении пределов. Простой прием раскрытия неопределенностей вида   и  дает правило Лопиталя, сущность которого заключается в следующей теореме.  Теорема.Предел отношения двух бесконечно малых или бесконечно больших функций при x → x₀равен пределу отношения их производных, если последний существует, то есть  (K может быть конечным и бесконечным).