30. Производные основных элементарных функций

Опираясь на математическое определение производной (1.6), а также на ее физический (1.7) и геометрический (1.11) смысл, можно найти производные всех основных элементарных функций.

Пример 1. Пусть y=f(x)=C (С – произвольная константа). Найдем производную y′ этой функции. То есть найдем производную C′ константы С.

Решение. Его можно получить тремя способами.

а) Способ 1 – геометрический.

Графиком функции y=C является горизонтальная прямая. Касательной к этой прямой, проведенной в любой ее точке, будет она сама. Ее угол наклона α к оси ох равен нулю. Но tg0=0. Значит, согласно (1.11), y′=C′=0.

б) Способ 2 – физический.

Функция y=C от x не зависит, то есть с изменением x не меняется. А значит, скорость v(x) ее изменения равна нулю. Но ведь скорость изменения функции, согласно (1.7) – это производная функции. Таким образом, если y=C, то y′=C′=0. Физический смысл этого вывода очевиден: если координата y движущейся точки неизменна, то точка стоит. А значит, скорость ее движения равна нулю.

в) Способ 3 – математический.

Воспользуемся математическим определением (1.6) производной функции:

             

Итак, разными способами получаем один и тот же вывод: если y=C, то y′=C′=0.

Пример 2. Пусть y=f(x)=x. Найдем производную y′=x′ этой функции.

Решение. Его наиболее просто получить геометрическим способом. Графиком функции y=x является прямая, представляющая собой биссектрису первого и третьего координатных углов. Ее угол наклона к оси ох составляет 45º. Касательная к этой прямой в любой ее точке (при любом x) совпадает с этой же прямой. Поэтому, опираясь на геометрический смысл производной (1.11), получаем: y′=x′=tg45º=1. То есть x′=1. Этот же результат, заметим, следует и из математического определения производной (1.6):

                                   

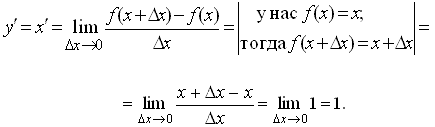
Пример 3. Пусть y=f(x)=x². Найдем производную y′ =(x²)′ этой функции.

Решение. Графиком функции y=x² является парабола. Касательная к ней в разных ее точках имеет разное направление (разный угол наклона  α к оси ох). Поэтому использовать геометрическую формулу (1.11) для нахождения производной этой функции в данном случае затруднительно. Затруднительно использовать и физический смысл производной (1.7). Тогда остается воспользоваться её математическим определением (1.6):

                   

Итак, если y=x², то y′ =(x²)′ =2x.

Используя математическое определение производной (1.6), можно найти производные всех основных элементарных функций. 

31. Правило дифференцирования функций, заданных параметрически

Зависимость функции y от аргумента x может осуществляться через посредство третьей переменной t, называемой параметром:

В этом случае говорят, что функция y от x задана параметрически. Параметрическое задание функции удобно тем, что оно дает общую запись для прямой и обратной функций.  Предположим, что на некотором промежутке функции x=φ(t) и y=ψ(t) имеют производные, причем φ’(t)≠0. Кроме того, для x=φ(t) существует обратная функция x^-1 = t(x) (производная обратной функции равна обратной величине производной прямой функции).  Тогда y(x)=ψ(t(x)) – сложная функция и ее производная: 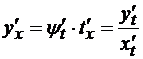 . Производную тоже запишем в параметрической форме: