Вопрос №10. Расширенная матрица слау. Элементарные преобразования расширенной матрицы слау.

Расширенная матрица СЛАУ:

[A_B] – расширенная матрица-система

А= X= B=

А_В =

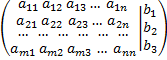
Элементарные преобразования расширенной матрицы СЛАУ:

1 – перемены местами любых столбцов матрицы А и любых строк расширенной матрицы А_В всегда допустимо.

2 – можно удалять нулевые строки, одну из одинаковых строк, и строки, элементы которых пропорциональны.

3 – любую строку расширенной матрицы А_В можно умножить на отличное от 0 число.

4 – допустимо прибавлять к элементам строки элементы другой строки, умноженные на произвольное число.

Вопрос №11 Метод Гаусса для решения слау.

Метод Гаусса – метод последовательного исключения переменных, заключающийся в том, что с помощью элементарных преобразований система приводится к ступенчатому виду, из которой по порядку, начиная с самого последнего номера, находятся все переменные.

При решении системы методом Гаусса выполняется прямой и обратный ход, а затем следует проверка:

1. При прямом ходе: расширенная матрица-система приводится к ступенчатому виду;

2. При обратном ходе последовательно находятся переменные;

3. Проверка.

Вопрос №12 Ранг матрицы. Теорема Кронекера-Капелли.

Ранг матрицы:

Рангом произвольной матрицы А, приведенной к каноническому виду, называется минимальное число из не нулевых строк или столбцов.

Rang A = min(m,n)

где m – кол-во ненулевых строк, n – кол-во ненулевых столбцов.

Теорема Кронекера-Капелли:

Система уравнений является совместной тогда и только тогда, когда ранг расширенной матрицы А_В равен рангу матрицы А.

Rang A_B = Rang A

1. Если ранг матрицы А (Rang A) = числу совместных неизвестных переменных, то система определенная

2. Если Rang A < n(n – кол-во неизвестных), то система неопределенная.

Вопрос №13 Геометрический вектор. Нулевой и противоположный векторы. Модуль вектора. Коллинеарные и компланарные вектора.

Вектор имеет направление и характеризуется длинной, которая называется модулем.

Геометрический вектор – направленный отрезок.

Если длина вектора =0, то он называется нулевым. Его направление можно считать произвольным.

Вектор «–а» можно считать противоположным вектором для вектора «а», если он имеет такую же длину, но противоположное направление.

Модуль – длина вектора.

Если 2 вектора лежат на 1 прямой или на параллельных прямых, то они называются коллинеарными.

Вектора называются компланарными, если они лежат на 1 плоскости или на параллельных плоскостях.

Вопрос №14 Линейные операции над геометрическими векторами.

• Сложение векторов:

Правило параллелограмма: суммой 2-ух вектором «а» и «в», имеющих общее начало, называется вектор «с», представляющий собой диагональ параллелограмма, построенного на векторах «а» и «в».

Правило треугольника: суммой векторов «а» и «в» называется вектор «с», проведенный из начала вектора «а» в конец вектора «в».

Свойства векторов: 1. а+в = в+а – свойство коммуникативности

2. (а+в)+с = а+(в+с) – свойство ассоциативности

3. а *0 = а – закон поглощения нуля.

• Разность векторов:

Разностью векторов «а» и «в» называется вектор «с», который в сумме с вектором «в» дает вектор «а»

• Умножение вектора на число

Произведением вектора «а» на число λ называется вектор «в», коллинеарным вектору «а», имеющий длину |в|=λ*|а|, и совпадающий по направлению с вектором «а», если λ положительная, и имеющий противоположное направление с вектором «а», если λ отрицательная.