Вопрос №1

Понятие матрицы. Виды матриц. Транспонирование матриц.

Определение

Определением матрицы размером m х n называется прямоугольная таблица чисел, состоящая из m строк и n столбцов. Числа, содержащиеся в матрице, называются элементами матрицы.

Структура матрицы:

А

mxn

= =

Общий вид матрицы:

А

I = 1,m

J = 1,n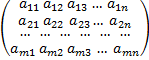

= = (a_ij)

Виды матриц:

1. Если матрица имеет 1 столбец – матрица-столбец.(m=1)

2. Если матрица имеет 1 сточку – матрица-строка.(n=1)

3. Матрица с одинаковым числом строк и столбцов – квадратная матрица. (m=n)

4. Квадратная матрица называется симметричной, если а_ij = а_ji

5. Элементы матрицы а_ij(при i=j)называются диагональными элементами

Диагональные элементы образуют главную диагональ

Квадратная матрица является диагональной, если элементы главн. диагонали не =0, а остальные =0.

6. Диагональная матрица явл. единичной, если у нее по диагонали стоят единицы.

7. Квадратная матрица называется верхне-треугольной, если все эл-ты, стоящие ниже главной диагонали,=0, и нижнее-треугольной, если эл-ты, стоящие выше главной диагонали, =0.

8. Нулевой матрицей называется матрица, состоящая только из нулей.

9. Если у матрицы поменять местами строки и столбцы, то получится транспонированная матрица.

Транспонированная матрица:

Транспонированной называется матрица, у которой поменяны местами строки и столбцы.

(первый столбец становится первой строкой, второй столбец второй строкой и т.д.)

Вопрос №2 Линейные действия над матрицами

Сумма:

Суммой матриц А и В одинаковой размерности называется матрица С такой же размерности, такая что:

С

mxn

mxn

mxn

= А + В

С

i= 1,m

j = 1,n

i = 1,m

j = 1,n

_ij =(а_ij + b_ij)

Разность:

Разность матриц А и В вводится аналогично сумме, только знаки эл-тов матрицы В меняются на противоположные:

С

mxn

mxn

mxn

= А - В

С

i= 1,m

j = 1,n

i = 1,m

j = 1,n

_ij =(а_ij + (-b_ji))

Произведение:

Пусть L – это число. Произведением L на А называется матрица С:

С

mxn

i= 1,m

j = 1,n

mxn

= L A = (L*a_ij)

Вопрос №3 Свойства линейных операций над матрицами

1 закон – коммуникативный (переместительный) закон сложения матриц: А+В = В+А

2 закон – ассоциативный (сочетательный) закон сложения матриц: А+(В+С) = (А+В)+С

3 закон – сочетательный закон произведения чисел на матрицу: L*(β*A) = (L*β)*A где L и β – числа 4 закон – распределительный закон умножения числе на матрицу и матрицы на число: (L+β)*A = L*A + β*A; (A+B)*L = L*A + L*B

Вопрос №4 Соответственные матрицы. Перемножение матриц.

Соответственные матрицы:

mxn

nxp

А * В – соответственные матрицы, число столбцов матрицы А = числу строк в матрице В

Произведение матриц:

Произведением матрицы А на матрицу В считается матрица С такая, что:

С

mxn

nxp

mxp

= А * В = С

С_ij = a_i1 * b_1j + a_i2 * b_2j + … a_in * b_nj = a_is * b_sj

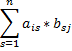
Вопрос №5. Определитель матрицы. Определители квадратных матриц 1-го, 2-го и 3-го порядков.

Определитель:

Определителем (детерминантом) называется число, которое ставится в соответствие этой матрицы и вычисляется по определенному правилу.

Определители 1-го, 2-го и 3-го порядков:

• 1-й порядок

А = (а₁₁) – определителем 1-го порядка называется число, равное единственному элементу этой матрицы: = det(А) = |А| = |a₁₁|=а₁₁

• 2-й порядок

А = - определителем 2-го порядка называется число, которое вычисляется по след. плавилу:

= det(A)=|A|= =a₁₁*a₂₂ – a₁₂*a₂₁

• 3-й порядок

А= – определителем 3-го порядка называется число, которое вычисляется по след. правилу:

= det(A)=|A|= a₁₁*a₂₂*a₃₃ + a₁₂*a₂₃*a₃₁ + a₂₁*a₃₂*a₁₃ – a₃₁*a₂₂*a₁₃ – a₂₁*a₁₂*a₃₃ – a₃₂*a₂₃*a₁₁

Правило Сарруса:

a₁₁ a₁₂ a₁₃

a₂₁ a₂₂ a₂₃

a₃₁ a₃₂ a₃₃

+ -

а ₁₁ а₁₂ а₁₃

а ₂₁ а₂₂ а₂₃

а₃₁ а₃₂ а₃₃

Правило диагоналей:

+ -

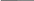
а

(a₁₁*a₂₂*a₃₃)+(a₁₂*a₂₃*a₃₁)+(a₁₃*a₂₁*a₃₂) –

-(a₃₁*a₂₂*a₁₃) – (a₃₂*a₂₃*a₁₁) – (a₃₃*a₂₁*a₁₂)

₁₁ а₁₂ а₁₃ a₁₁ a12

a₁₁ a₁₂ a₁₃ a₁₁ a₁₂

а₂₁ а₂₂ а₂₃ a₂₁ a₂₂

а₃₁ а₃₂ а₃₃ a₃₁ a₃₂

а₂₁ а₂₂ а₂₃ a₂₁ a₂₂

а₃₁ а₃₂ а₃₃ a₃₁ a₃₂