1.7. Макроскопические свойства материи

Итак, известны основные уравнения Максвелла:

(1.37)

В этих уравнениях имеются только независимые векторы, вещества же совсем нет. Но присутствие среды меняет определённым образом поле. Поэтому необходимо получить зависимость свойств поля от среды (вещества). Будем считать, что если никакой внешний заряд не внесён в среду, то среда считается нейтральной.

Влияние свойств среды должно обусловить определённые соотношения между векторами электрического поля и и между векторами магнитного поля и . В рамках макроскопической теории об этих соотношениях могут быть высказаны лишь предположения, справедливость которых подтверждается лишь опытной проверкой [8].

С точки зрения электромагнитных свойств сред их можно разделить на две категории: изотропные и анизотропные среды.

Изотропные среды – это такие среды, свойства которых в окрестностях данной точки не зависят от направления, но могут меняться от точки к точке. Изотропная среда, свойства которой не меняются от точки к точке, называется однородной. В противном случае среда называется неоднородной.

Анизотропные среды – такие среды, свойства которых в окрестностях данной точки неодинаковы в различных направлениях. Это чаще всего кристаллические тела.

Для изотропных сред естественно предположить, что между векторами и , и выполняется простейшая зависимость:

где – абсолютная диэлектрическая проницаемость среды, Ф/м;

– абсолютная магнитная проницаемость среды, Гн/м.

Могут наблюдаться два сорта тел, в которых и зависят соответственно от и . В этом случае зависимости становятся нелинейными и решение уравнений Максвелла сложны, и среды в которых и не зависят от и В этом случае уравнения Максвелла решаются значительно проще. Мы в основном будем рассматривать этот случай.

Единственной действительно изотропной средой является вакуум, так как там никаких зарядов нет. Абсолютные проницаемости вакуума обозначим и . Напомним, что в системе интернациональной СИ

;

Абсолютные проницаемости вещества, отнесённые к абсолютной проницаемости вакуума, называются относительными проницаемостями. Обозначим их через и . Тогда

Для вакуума

Отметим, что для твёрдых и жидких тел с малой ионизацией между плотностью тока проводимости и напряжённостью электрического поля существует линейная зависимость

(1.38)

где – удельная электропроводность среды или удельная проводимость среды.

Характерной особенностью этой проводимости является то, что диапазон её возможных значений чрезвычайно велик. Выражение (1.38) есть дифференциальный закон Ома.

1.8. Граничные условия

На практике имеем дело не с бесконечно однородными, а с кусочно-однородными телами. При применении формул преобразования (Остроградского и Стокса) мы оговаривали, что их непосредственное использование требует конечности и непрерывности подынтегральной функции и их производных как внутри области интегрирования, так и на её границе. В связи с этим уравнения Максвелла имеют место только в обыкновенных точках поля, в которых все векторы и функции конечны и непрерывны вместе со своими производными.

Однако в пространстве, заполненном веществом, могут существовать особые поверхности, в точках которых векторные и скалярные функции, введённые теорией для описания электромагнитного поля, и их производные терпят разрыв непрерывности. Такими особыми поверхностями являются поверхности соприкосновения (заряженные или незаряженные) или границы раздела между средами с различными параметрами , .

Существует общий математический приём: вначале эти точки или поверхности исключают из рассмотрения, а потом делают предельный переход, если он даёт результат.

Граничные условия для нормальных составляющих векторов , :

а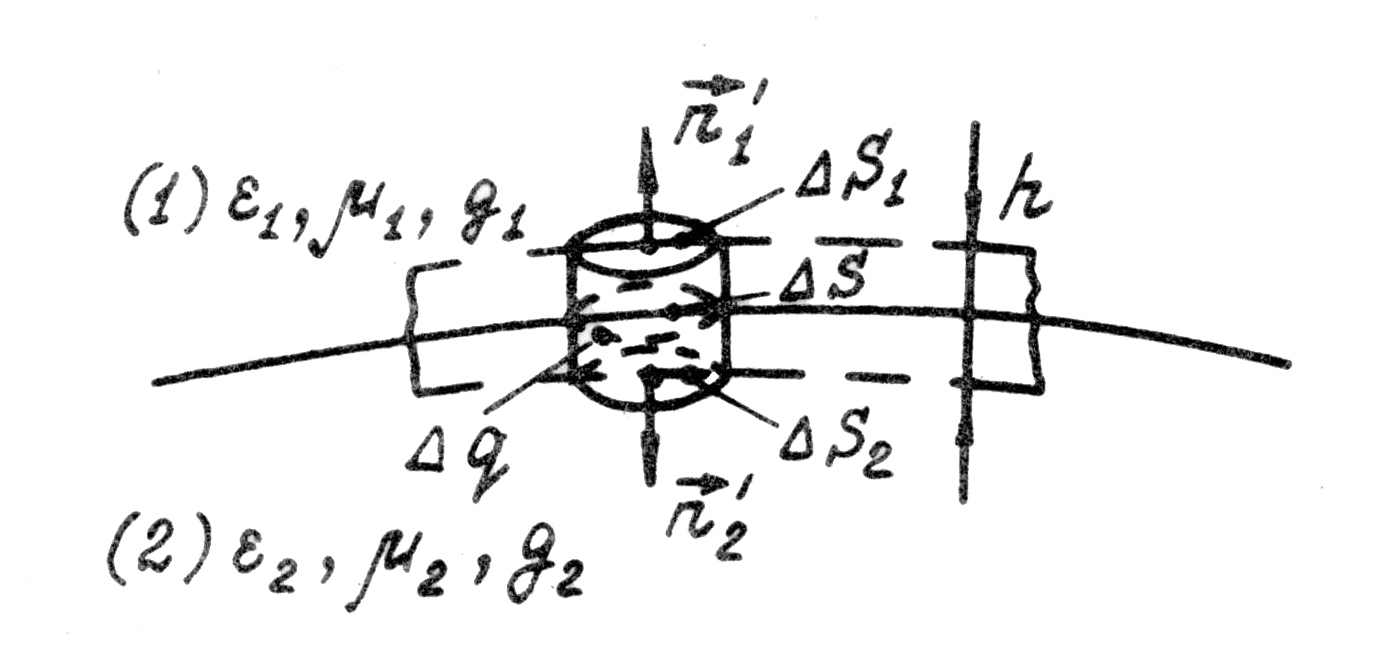 ) Имеем поверхность соприкосновения (границу раздела) двух сред (рис. 1.8).

Рис. 1.8

Заменим эту поверхность конечным слоем и построим в этом слое элементарный цилиндр. Проведём нормали и . Параметры внутри слоя достаточно быстро меняются от значений , до значений , . Для выделенного цилиндра запишем постулат Максвелла

Так как цилиндр очень маленький (элементарный), то поток вектора можно записать по частям, взяв средние значения.

где – среднее значение нормальной составляющей вектора в первой среде через площадку ;

– среднее значение нормальной составляющей вектора во второй среде через площадку ;

– поток вектора через боковую поверхность цилиндра;

– заряд внутри цилиндра.

Будем сжимать слой до поверхности (до нуля), т. е. При

причём .

Поэтому при получим:

Отсюда

где – среднее значение поверхностной плотности заряда.

Теперь устремим т. е. возьмём пределы от левой и правой частей последнего равенства при Нетрудно заметить, что при

В результате такого предельного перехода получим:

(1.39)

.

Выражение (1.39) представляет граничное условие для нормальных составляющих вектора на границе раздела двух сред с конечными значениями , .

Если спроектировать вектор на какую-либо одну из нормалей или , и учитывая, что , то получим:

В

(1.40)

проекции на

В

(1.41)

проекции на

Формулы (1.40) и (1.41) представляют разновидности граничного условия (1.39) для нормальных составляющих вектора .

б) Получим граничное условие для нормальной составляющей вектора .

Известно, что . Тогда в соответствии с формулой Остроградского

получим, что и

Рассуждая аналогично, как и для вектора получим:

(1.42)

Формула (1.42) представляет граничное условие для нормальных составляющих вектора

в) Аналогично рассмотренным случаям получим граничное условие для нормальных составляющих вектора плотности полного тока .

Известно, что . Применяя формулу Остроградского

получим, что и

Следовательно,

Ф

(1.43)

ормула (1.43) и есть граничное условие для нормальных составляющих вектора

Граничные условия, выраженные формулами (1.39), (1.42) и (1.43), формулируются следующим образом: при переходе через границу раздела между двумя средами с различными параметрами нормальная к поверхности составляющая вектора терпит разрыв непрерывности, равный по величине поверхностной плотности заряда . Нормальные же составляющие векторов и остаются непрерывными.

Рассмотрим некоторые, встречающиеся на практике случаи граничных условий, которые следуют из формул (1.39), (1.42), (1.43).

1. Если поверхность раздела не заряжена т. е.

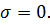
В этом случае в соответствии с (1.39) нормальная составляющая вектора остаётся непрерывной. В рассматриваемых нами изотропных средах, как известно,

.

Из (1.39) и (1.42) имеем

или

Следовательно, нормальная составляющая вектора на границе раздела сред с различными параметрами терпит разрыв непрерывности и в том случае, когда поверхность не заряжена ( ). Так же терпит разрыв непрерывности и нормальная составляющая вектора , если .

2. Получены граничные условия , а Известно так же, что .

Учитывая данные равенства и выражение (1.38) , можно записать:

(1.44)

Если то нормальная составляющая объёмной плотности тока проводимости на поверхности раздела двух сред терпит разрыв непрерывности, равный по величине производной по времени от поверхностной плотности заряда , взятой с обратным знаком.

3) Выясним теперь, при каких условиях поверхностный заряд существует и при каких отсутствует. Это важно при введении в теорию идеализированных сред (идеальные диэлектрики и идеальные проводники ), которые находят широкое применение в практических расчётах, так как при этом решение задач значительно упрощается и во многих случаях приводит к вполне удовлетворительным по точности результатам.

Нам уже известно, что

Если , то при отличных от нуля нормальных составляющих вектора должно выполняться условие:

(1.45)

, т. е.

Следовательно, при произвольных, отличных от нуля параметров и соприкасающихся сред, поверхностная плотность зарядов на границе раздела всегда отлична от нуля, за исключением тех частных случаев, когда параметры соприкасающихся сред удовлетворяют уравнению (1.45).

Если же одна из сред является идеальным диэлектриком, например, , то уравнение (1.45) не удовлетворяется и, следовательно, . При этом уравнение (1.44) соответствует уравнению непрерывности потока зарядов к границе раздела. Очевидно, и в том случае, когда одна из сред является идеальным проводником ( ).

Во всех этих случаях поверхностные заряды являются индуктированными в проводящей среде нормальной составляющей вектора . В этом случае, когда обе соприкасающиеся среды – идеальные диэлектрики ( , поверхностная плотность заряда , если только поверхность раздела специально не заряжена.

Граничные условия для тангенциальных составляющих векторов и .

Для получения этих граничных условий воспользуемся интегральным выражением закона полного тока. Пусть имеем поверхность раздела двух сред (рис. 1.9). Расширим её до слоя. Возьмём тройку единичных векторов , тогда

Задаёмся направлением обхода элементарного контура. Приближённо можно записать:

где и – среднее значение вектора на и ;

– интеграл по боковым сторонам.

Будем сжимать слой до нуля, т. е. тогда

Получим

.

Д

(1.46)

ля сред с конечными параметрами . Так как и – конечные величины, то и конечная. Для реальных физических полей и – конечная величина. Следовательно при стягивании контура в точку, т. е. и получим:

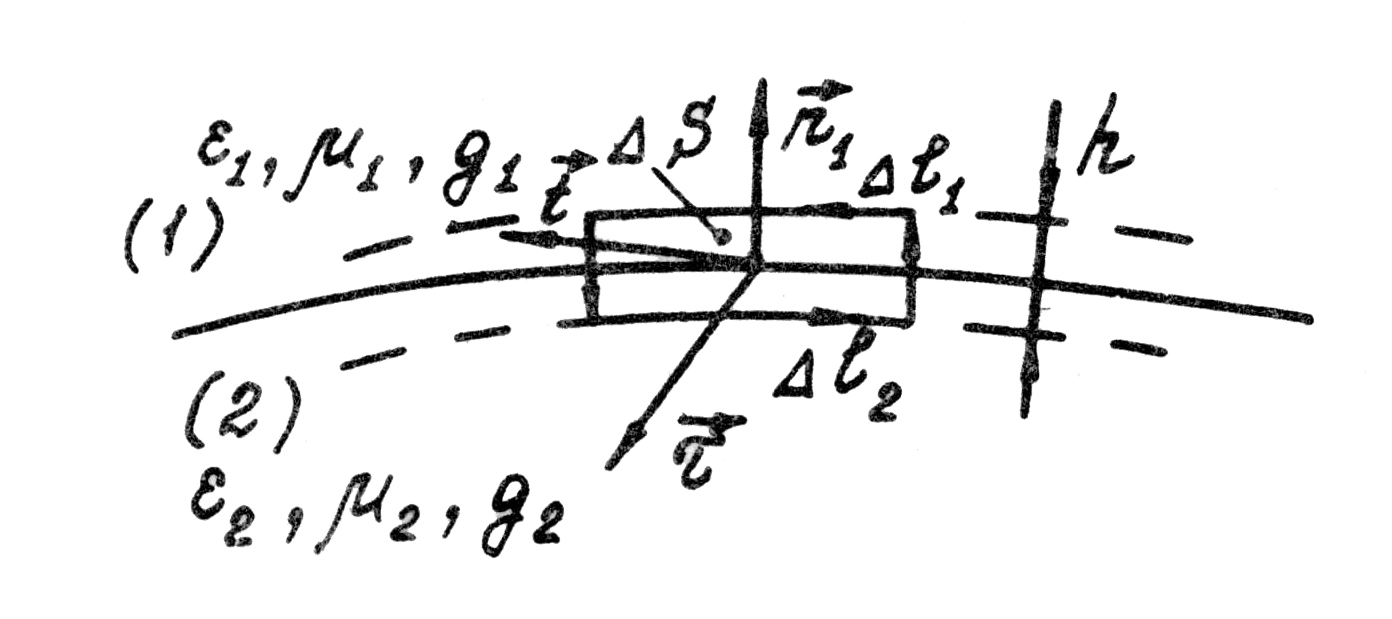
Рис. 1.9

Выражение (1.46) есть граничное условие для тангенциальных составляющих вектора для сред с конечными параметрами. Применив к этому же контуру (см. рис. 1.9) закон электромагнитной индукции

и полагая, что вектор и его производные всегда конечны, уже без ограничений на параметры сред получим:

(1.47)

Формула (1.47) есть граничное условие для тангенциальных составляющих вектора на поверхности раздела двух сред.

Граничные условия (1.46) и (1.47) формулируются следующим образом: при переходе границы раздела между двумя средами, имеющими конечные параметры , , тангенциальные составляющие векторов и остаются непрерывными.

Рассмотрим некоторые встречающиеся на практике случаи граничных условий, которые следуют из рассмотренных соотношений.

1. Граничные условия для тангенциальных составляющих векторов и .

Можно записать, что

На основании (1.47) имеем:

(1.48)

или .

Из формулы (1.48) следует, что тангенциальные составляющие вектора на границе раздела терпят разрыв непрерывности.

Тангенциальные составляющие вектора терпят разрыв непрерывности на границе раздела сред, для которых

2. Граничные условия на поверхности идеального проводника.

Если одна из сред является идеально проводящей , то вывод граничных условий необходимо пересмотреть. Обратимся к уравнению Максвелла

(1.49)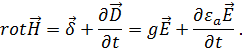

Замечаем, что при и конечном значении . Так как ни бесконечные значения векторов, ни бесконечные значения их производных не могут отвечать реально существующим физическим полям, то мы должны принять невозможность существования электрического поля в идеально проводящей среде.

Но если в любой точке идеального проводника , то из уравнения следует, что Следовательно, в идеальном проводнике может существовать только постоянное (стационарное) магнитное поле

П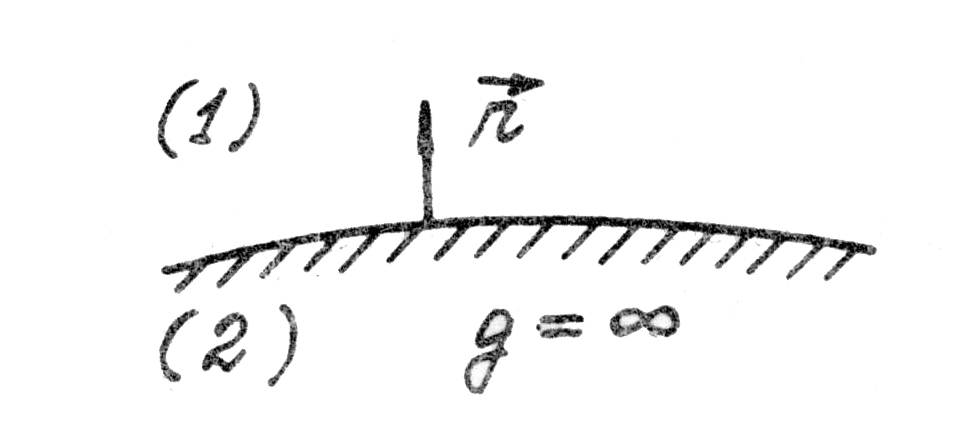 ри изучении явлений, связанных с переменным электромагнитным полем, наличие постоянной составляющей магнитного поля не имеет значения. Поэтому можно считать, что в идеальном проводнике электромагнитное поле существовать не может и в любой его внутренней точке и

Рис. 1.10

Учитывая это положение, запишем граничные условия на поверхности идеального проводника, соприкасающейся с любой средой, включая и (рис. 1.10)

(1.50)

Формулы (1.50) представляют граничные условия на поверхности идеального проводника.

Рассмотрим условие (1.46) для тангенциальной составляющей вектора на поверхности идеального проводника. То, что в идеально проводящей среде переменное электромагнитное поле существовать не может, исключает и возможность существования переменного тока, распределённого по всему идеально проводящему телу с объёмной плотностью . Этот результат находится в соответствии с явлением поверхностного эффекта, т. е. распределение объёмной плотности переменного тока проводимости по сечению проводника неравномерное. Оно возрастает по величине в точках более близких к поверхности проводника. Вытеснение тока к поверхности проводника возрастает с увеличением проводимости и частоты.

При весь ток собирается в бесконечно тонком поверхностном слое проводника. При этом объёмная плотность тока теряет смысл, так как стремится к бесконечности: , , – конечно, следовательно . В этом случае при получении условий (1.46) появляется неопределённость, так как ,

Раскроем эту неопределённость. Из рис. 1.9 следует, что через элементарную площадку протекает ток Если будем сжимать этот слой до поверхности, то при величина не должна измениться и, следовательно, – величина конечная. Называют эту величину поверхностной составляющей плотности тока проводимости в направлении единичного вектора или просто поверхностной плотностью тока, который обозначим через , т. е.

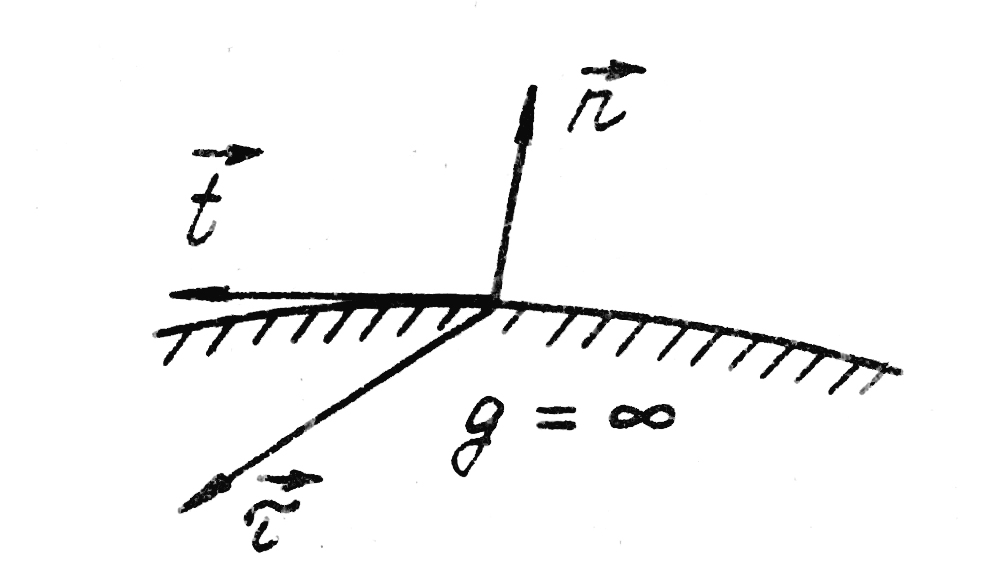В отличие от объёмной плотности тока , абсолютная величина которой определяет количество электричества, пересекающего в единицу времени единичную площадку, перпендикулярную вектору , поверхностная плотность тока определяет количество электричества, пересекающего в единицу времени единичную линию, перпендикулярную , лежащую на поверхности.

Рис. 1.11

На основании изложенного граничное условие для поверхности идеального проводника запишется в следующем виде:

(1.51)

При использовании формул (1.50) и (1.51) нужно помнить о принятом расположении тройки единичных векторов (рис. 1.11).

Условия (1.50) и (1.51) выражают: на поверхности идеального проводника тангенциальная составляющая вектора и нормальная составляющая вектора всегда равны нулю; нормальная составляющая вектора равна поверхностной плотности заряда на проводнике; тангенциальная составляющая вектора равна соответствующей составляющей вектора поверхностной плотности тока в проводнике.