§ 10. Оператор набла . Основные тождества векторного анализа

В § 7 был введён оператор Гамильтона или набла

Не останавливаясь на важных самостоятельных свойствах этого символического вектора, воспользуемся им лишь для более быстрого получения основных тождеств векторного анализа. Быстрота достигается тем, что при применении набла к скалярным и векторным функциям сохраняются все правила векторного исчисления.

Следует помнить, что выражаемая символом «набла» дифференциальная операция применяется лишь к тем величинам, которые стоят справа от него.

(17)

(18)

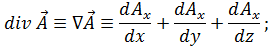
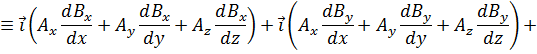
(21)

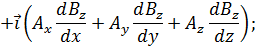
(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

(35)

(36)

(37)

(38)

(39)

(40)

В формулах (36), (37) и (38) – единичный вектор внешней нормали к заданной поверхности s, ограничивающей объём V; в формулах (39) и (40) – единичный вектор нормали к положительной стороне поверхности s, опирающейся на замкнутый контур l (положительной называется сторона, обращённая к наблюдателю, обходящему контур против часовой стрелки).

Для получения тождеств (29) – (35) следует помнить лишь правило дифференцирования произведения, согласно которому дифференцируется сначала первый множитель, а все остальные считают постоянными; затем дифференцируют только второй множитель, а все остальные считают постоянными и т. д.; все полученные выражения складывают. Во избежание ошибок удобно в каждом случае дифференцирования отмечать, например, индексом «с» (const) те множители, которые считаются постоянными.

Для примера рассмотрим тождества (31) и (32).

Имеем

Очевидно,

Отбрасывая ненужные теперь индексы и складывая, получаем (31).

Далее

Но по § 4, п. 2.

откуда и следует (32).

Заметим, что для получения правильного ответа нужно из возможных форм выражения брать то, в котором переменный множитель стоит справа от оператора набла.

Формулы (37) и (38) вытекают из формулы Остроградского (36).

Для получения формулы (37) нужно положить в формуле (36) , а для получения формулы (38) нужно положить в формуле (36) , где – произвольный постоянный вектор.

Формула (40) вытекает из формулы Стокса (39), если положить в ней , где – произвольный постоянный вектор.

Например, положим в формуле (36) . Тогда левая сторона формулы (36) примет вид

а правая сторона формулы (36) будет

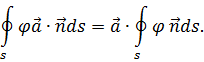
Приравнивая найденные выражения и сокращая постоянный вектор , получим формулу (37).

Литература

1. Баскаков С.И. Основы электродинамики. М.: Сов.радио, 1973.

2. Гольдштейн А.Д., Зернов Н.В. Электромагнитные поля и волны, М.: Сов. радио, 1971.

3. Гоноровский И.С. Радиотехнические цепи и сигналы. М.: Сов. радио, 1977.

4. Зернов Н.В., Карпов В.Г. Теория радиотехнических цепей. Л.: Энергия, 1972.

5. Марков С.Т., Петров Б.М., Грудинская Г.П. Электродинамика и распространение радиоволн. М.: Сов. радио, 1973.

6. Миролюбов Н.Н. Курс теоретических основ радиотехники. М.: МО, 1957.

7. Семёнов Н.А. Техническая электродинамика. М., 1973.

8. Швыркин Н.В. Радиотехника. М.: МО, 1978.