1.5. Закон электромагнитной индукции и его обобщение

Согласно закону Фарадея в замкнутом проводнике, помещённом в магнитное поле, возникает ЭДС, пропорциональна скорости изменения магнитного потока, пронизывающего этот контур,

(1.26)

Обобщим этот закон, чтобы найти соотношение между и в точке пространства.

Учитывая, что ЭДС в замкнутом контуре , а магнитный поток, пронизывающий площадь , ограниченную контуром , получим из (1.26):

(1.27)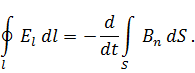

Наличие проводника позволяет лишь зафиксировать (обнаружить) ЭДС Таким образом, если имеем в пространстве переменное магнитное поле, то возникает и электрическое поле и они связаны соотношением

Интегрирование здесь ведётся по воображаемому контуру. Если будем рассматривать неподвижные среды, где магнитное поле меняется во времени, а контур фиксирован, то (1.27) можно переписать в виде:

(1.28)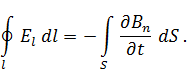

При условии непрерывности подынтегральных функций и, сделав предельный переход, аналогично, как в выражении (1.18) получим

(1.29)

Это дифференциальная форма закона электромагнитной индукции, связывающая и , в точке пространства. Подчеркнём, что из обобщений Максвелла вытекает исключительно важное представление о физической природе поля.

Существование электрического поля связано не только с наличием электрических зарядов, но для его возникновения также достаточно только изменения во времени магнитного поля.

Из (1.29) находим, что

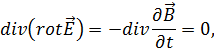
так как т. е. поэтому всегда Перестановка оператора и допустима, так как по предложению в обыкновенной точке поля вектор непрерывен со всеми своими производными.

Из постоянства дивергенции в любой точке поля следует, что если когда-либо в прошлом поле отсутствовало (т. е. было время, когда ), то и всегда Утверждение о том, что всегда находится в соответствии со сделанным ранее указанием на соленоидальность поля вектора , вследствие отсутствия истинного магнетизма (магнитных масс).

1.6. Ток смещения. Уравнения Максвелла

Стационарное (постоянное) электромагнитное поле – такое поле, которое с течением времени не меняется, т. е. Соберём все результаты, которые получили ранее, полагая

а) ;

(1.30)

б) ;

в) ;

г) ;

д)

При этом уравнение д) находится в полном соответствии с уравнением б), так как =0. Данные уравнения не имеют внутренних противоречий [6].

Переменное электромагнитное поле. В этом случае Уравнения а) и д) из (1.30) запишутся следующим образом:

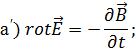
Если предположить, что уравнения б), в) и г) сохраняются и для переменного электромагнитного поля, то заметим, что уравнение а) совместимо с уравнением в); уравнение д) противоречит уравнению б). Следовательно, уравнение д) справедливо для постоянного тока, не справедливо для переменного тока.

Максвелл устранил это противоречие введением нового понятия – тока смещения и соответствующим обобщением закона полного тока.

Подставляя значение в уравнение из уравнения г), получим:

Следовательно,

(1.31)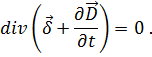

Таким образом, получили, что уже не , а всегда равна 0. Максвелл назвал вектором плотности тока смещения , т. е.

(1.32)

Обозначим

(1.33)

Вектор называется вектором объёмной плотности полного тока.

Причём всегда выполняется условие соленоидальности вектора :

(1.34)

В проводящей среде при изменяющемся во времени электромагнитном поле должны наблюдаться оба тока – ток проводимости и ток смещения. Следовательно, для переменного электромагнитного пол уравнение б) запишется более общим уравнением

При наличии же сторонних ЭДС нужно к добавить .

Таким образом, Максвелл составил наиболее общую систему уравнений переменного (нестационарного) электромагнитного поля, которая справедлива для стационарного поля, положив в ней :

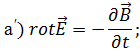
(1.35)

Уравнения (1.35) и есть уравнения Максвелла, которые лежат в основе теории электромагнитного поля. Из них уравнения – основные, уравнения и – их следствия, уравнение – уравнение непрерывности или дифференциальная форма закона сохранения электрического заряда. Заметим, что уравнения (1.30) для постоянного поля являются частным случаем уравнений (1.35).

Универсальность уравнений Максвелла заключается в том, что они не содержат никаких сред. Исключительно симметричный вид принимают уравнения (1.35) в случае идеального ( ) и незаряженного ( =0) диэлектрика (например, вакуум):

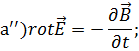
(1.36)

В этих уравнениях положено, что . Уравнения (1.36) можно применять во многих случаях и к реальным диэлектрикам, например, к воздуху. Уравнение соответствует тому, что переменное магнитное поле порождает электрическое поле. Уравнение соответствует тому, что переменное электрическое поле порождает магнитное поле.

Уравнения (1.36) дают отличные от нуля решения. Следовательно, может существовать электромагнитное поле независимо от его источника. Такое электромагнитное поле может быть только переменным. Это электромагнитное поле называется электромагнитными волнами.