Вопросы к главе 6

1. Общие сведения об излучении электромагнитных волн.

2. Поле излучения произвольно заданной системы токов.

3. Электрический вектор-потенциал произвольно заданной системы токов.

4. Электромагнитное поле электрического диполя.

5. Вектор-потенциал электрического диполя. Функция сферической волны.

6. Поле электрического диполя в ближней зоне.

7. Поле электрического диполя в промежуточной зоне.

8. Поле электрического диполя в дальней зоне.

9. Мощность и сопротивление излучения электрического диполя.

10. Рамочная антенна (магнитный диполь). Вектор-потенциал магнитного диполя.

11. Составляющие поля магнитного диполя.

12. Диаграмма направленности рамочной антенны.

13. Среднее значение вектора Умова – Пойнтинга для рамочной антенны.

14. Мощность и сопротивление излучения рамочной антенны.

15. Способы увеличения действующей высоты рамочной антенны.

Глава 7 длинные линии

7.1. Общие сведения

Длинные линии являются цепями с распределёнными параметрами, в которых напряжение и ток являются функциями как времени, так и координат. В таких цепях необходимо учитывать явление запаздывания электромагнитных колебаний.

В длинных линиях каждый её элементарный участок является носителем и электрической, и магнитной энергии, и энергии потерь одновременно.

Длинной называется такая линия, длина которой соизмерима с длиной волны колебаний, распространяющихся вдоль этой линии, т. е.

где – длина линии;

– длина волны.

Например, линия электропередачи длиной = 1000 км на частоте = 50 Гц не является длинной, так как

где – скорость света;

– период колебаний,

т. е. имеет место неравенство .

Линия же длиной = 10 м на частоте = 100 МГц является длинной, так как

и выполняется, следовательно, условие .

Из приведенных примеров видно, что понятие длинной линии – понятие относительное.

Отношение называется электрической длиной длинной линии. Существует несколько видов длинных линий, различающихся по конструкции. Простейшими из них являются:

двухпроводная открытая, симметричная длинная линия (рис. 1.1а), образованная двумя параллельными цилиндрическими проводами;

коаксиальная длинная линия (коаксиальный кабель) (рис. 1.16), состоящая из двух концентрических цилиндрических проводников, пространство между которыми заполнено воздухом или диэлектриком;

з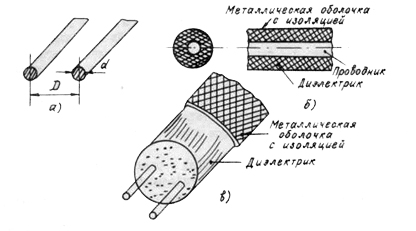 акрытая двухпроводная линия (рис. 1.1в), образованная двумя параллельными цилиндрическими проводами, находящимися в диэлектрике и окружёнными металлической оболочкой. Имеются и другие разновидности длинных линий.

Рис. 7.1

В длинных линиях индуктивность , ёмкость , активное сопротивление и проводимость не сосредоточены в определенных элементах, а распределены по длине линии.

Цепи, в которых и – распределены по длине линии, называются цепями с распределёнными параметрами.

Электрические процессы в цепях с распределёнными параметрами существенно отличаются от процессов в цепях с сосредоточенными параметрами. В цепях с распределёнными параметрами нельзя пренебречь эффектом запаздывания (задержкой во времени) в передаче сигналов. В силу этого напряжения и ток в длинной линии для каждого момента времени будут различными для различных сечений.

Несмотря на конструктивные различия длинных линий, с теоретической точки зрения любую линию можно рассматривать как двухпроводную линию. Отличие заключается только в погонных параметрах:

– погонная индуктивность;

– погонная ёмкость;

– погонное сопротивление потерь;

– погонная проводимость утечки, т. е. в параметрах, приходящихся на единицу длины линий.

Если погонные параметры не меняются по всей длине линии, то линия называется однородной. В противном случае линия называется неоднородной. Далее будут рассматриваться только одно­родные длинные линии.

Цепи с распределёнными параметрами играют важную роль в современной радиотехнике. Во многих устройствах подобные цепи находят применение для передачи высокочастотной электромагнитной энергии, например, от радиопередатчика к антенне, от антенны к радиоприёмнику и т. д. Отрезки длинных линий используются в качестве колебательных систем и полосовых фильтров. При помощи линий можно измерять многие радиотехнические параметры (длины волн, частоты колебаний, активные и реактивные сопротивления и др.).

Широкое применение длинных линий в радиотехнике повлекло за собой их быструю разработку. Значительный вклад в развитие теории длинных линий внесли советские учёные А.А. Пистолькорс, В.В. Татаринов, М.С. Нейман и другие.

Основными уравнениями длинной линии являются дифференциальные (телеграфные) уравнения напряжения и тока в длинной линии.