1.4. Вектор напряжённости магнитного поля и вектор магнитной индукции

Опытом установлено, что между точечными магнитными массами имеет место взаимодействие, аналогично закону Кулона.

где – коэффициент, зависящий от свойств среды и выбора системы единиц;

–магнитные массы взаимодействующих полюсов;

– расстояние между и .

Аналогично электрическому полю вводится понятие напряжённости магнитного поля:

(1.17)

где – напряжённость магнитного поля.

Напряжённость магнитного поля есть сила, действующая на единичный точечный магнитный заряд, помещённый в данную точку магнитного поля. Из (1.17) видно, что зависит от свойств среды. Продолжая аналогию с электрическим полем, можно ввести и понятие вектора магнитной индукции , связанного с магнитной массой соотношением, аналогичным постулату Максвелла:

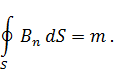
Экспериментально установлено, что при протекании по проводнику постоянного электрического тока вокруг него образуется магнитное поле и его особенностями являются:

линии магнитного поля всегда замкнуты (рис 1.6); между напряжённостью магнитного поля и током в проводнике независимо от свойств окружающей среды имеет место закон полного тока или закон магнитодвижущей силы (МДС):

т. е. циркуляция вектора напряженности магнитного поля равна току, если контур интегрирования охватывает проводник, если же контур интегрирования не охватывает проводник с током, то

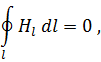
Проводник с током испытывает механическое взаимодействие с магнитным полем, полученным каким-либо другим способом (см. рис. 1.6), и сила взаимодействия равна:

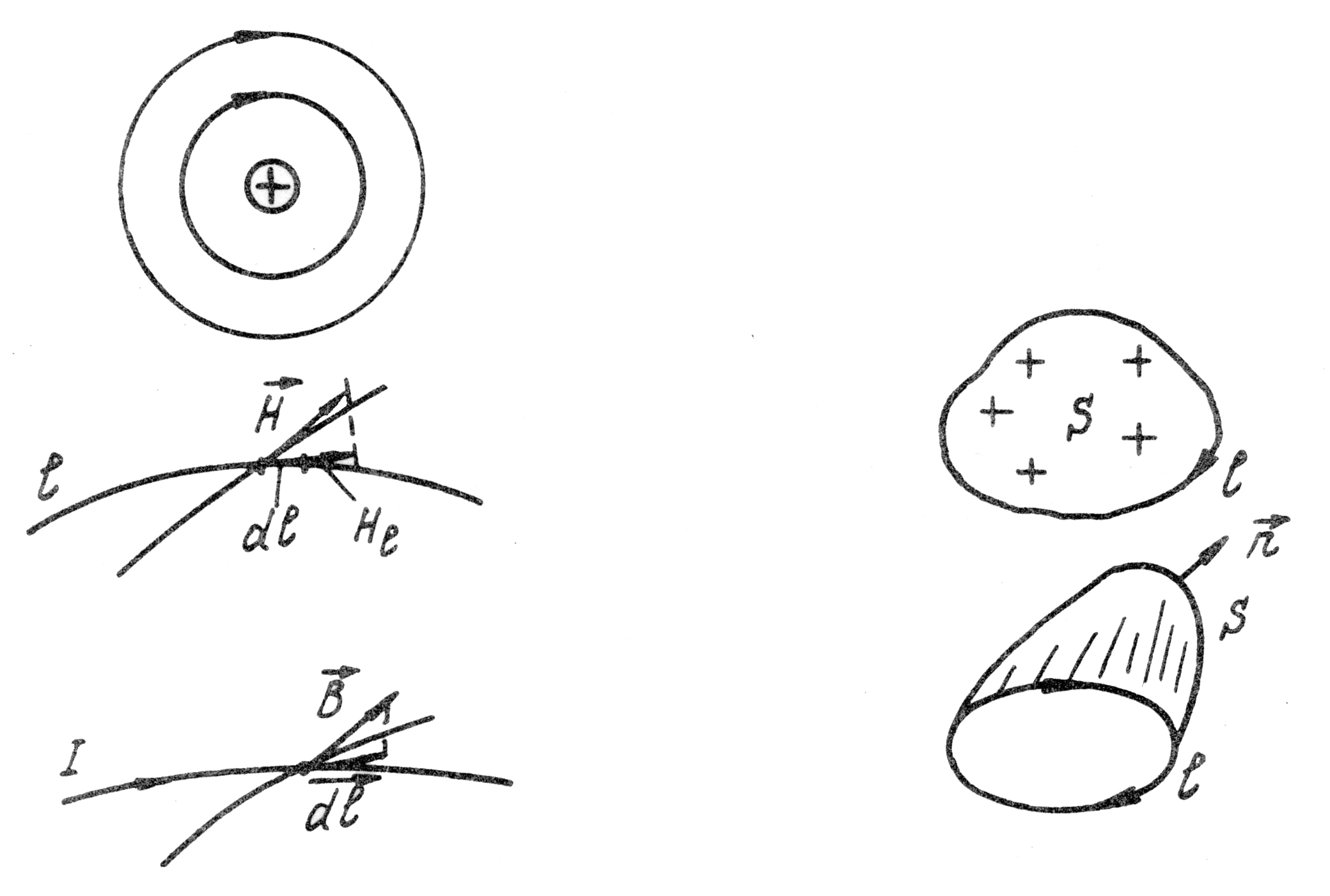
Рис. 1.6 Рис. 1.7

Эти факты позволяют уточнить свойства магнитного поля:

поток вектора через замкнутую поверхность всегда равен нулю. Этот принцип непрерывности (замкнутости) магнитных линий выражается уравнением

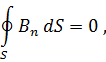
т. е. сколько линий входит в данную поверхность, столько и выходит. Следовательно, на основании формулы Остроградского (1.11) в случае непрерывности вектора и его производных внутри области и на её поверхности имеем:

Это говорит о том, что никаких магнитных масс не существует. Источником магнитного поля является движущийся заряд (ток).

Для описания магнитного поля основным является вектор магнитной индукции , так как он находится в соответствии с физической природой магнитного поля и основным принципом непрерывности (замкнутости) линий этого поля.

Однако мы сохраним напряжённость магнитного поля , так как она входит в закон полного тока. Максвелл обобщил закон полного тока в том смысле, что он выполняется при любом распределении тока внутри произвольно воображаемого замкнутого контура (рис. 1.7) и может быть записан:

(1.18)

слева интеграл по замкнутому контуру, а справа – интеграл по поверхности, опирающийся на этот контур. Для выполнения соотношения знаков необходимо указывать направления интегрирования и направления тока. Для бесконечно малого контура можно записать

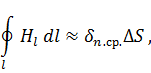
где – среднее значение нормальной составляющей вектора плотности тока.

Если , то формула будет точной. Рассмотрим предел отношения

(1.19)

Предел этого отношения в математике известен как ротор (вихрь) вектора (в данном случае вектора ):

где – проекция ротора вектора на нормаль к площадке в точке. Этот предел равен проекции вектора плотности тока на нормаль к площадке (нормаль и обход контура направлены по правилу правого винта).

Наибольшее значение плотности тока имеет место тогда, когда направление вектора совпадает с направлением вектора , т. е. когда лини тока перпендикулярны площадке в окрестности данной точки. В этом случае из (1.19) следует, что

(1.20)

Ротор равен току проводимости. Выражение (1.20) представляет дифференциальную форму закона полного тока. В прямоугольной системе координат

Если вектор непрерывен вместе со своими производными во всех точках контура и на опирающейся на него поверхности , то на основании (1.18) с учётом (1.19) получим:

(1.21)

Выражение (1.21) известно в математике как формула Стокса.

Рассматривая вектор магнитной индукции , приведём выражение для силы, определяющей действие магнитного поля на движущийся со скоростью электрический заряд .

Известно, что сила, действующая на проводник, помещённый в магнитное поле, равна:

где – элемент проводника.

Но ток

Следовательно,

Знак минус указывает, что ток противоположен движению электронов. Сила действующая на один электрон, равна:

(1.22)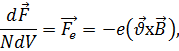

где сила Лоренца.

С

(1.23)

ила же действующая на элементарный заряд , определится

Из анализа выражения (1.23) следует, что эта сила меняет только направление движения заряда. Сила же действия электрического поля на заряд , как известно, определяется:

(1.24)

Эта сила имеет такое же направление, как и вектор . Полная же сила, действующая на заряд , при взаимодействии этого заряда с электрическими и магнитными полями равна:

(1.25)

Эта формула находит широкое применения при рассмотрении распространения радиоволн в ионизированных анизотропных средах и явлений, происходящих в электронных приборах.