6.6. Рамочная антенна. Магнитный диполь

Простейшей рамочной антенной является прямоугольный или круговой витки провода (рис. 6.8). Будем полагать, что линейные размеры витка малы по сравнению с длиной волны. В этом случае распределение тока вдоль витка будет примерно постоянным [6].

Основные свойства направленности излучения рамочной антенны легко установить на основании простых геометрических соображений. Пусть рамка имеет прямоугольную форму (рис. 6.8). В направлении, перпендикулярном плоскости рамки, излучения не будет, так как расстояние от любых двух симметричных элементов витка (плечи 1 – 3, 2 – 4) с противоположно направленными токами до оси одинаковы.

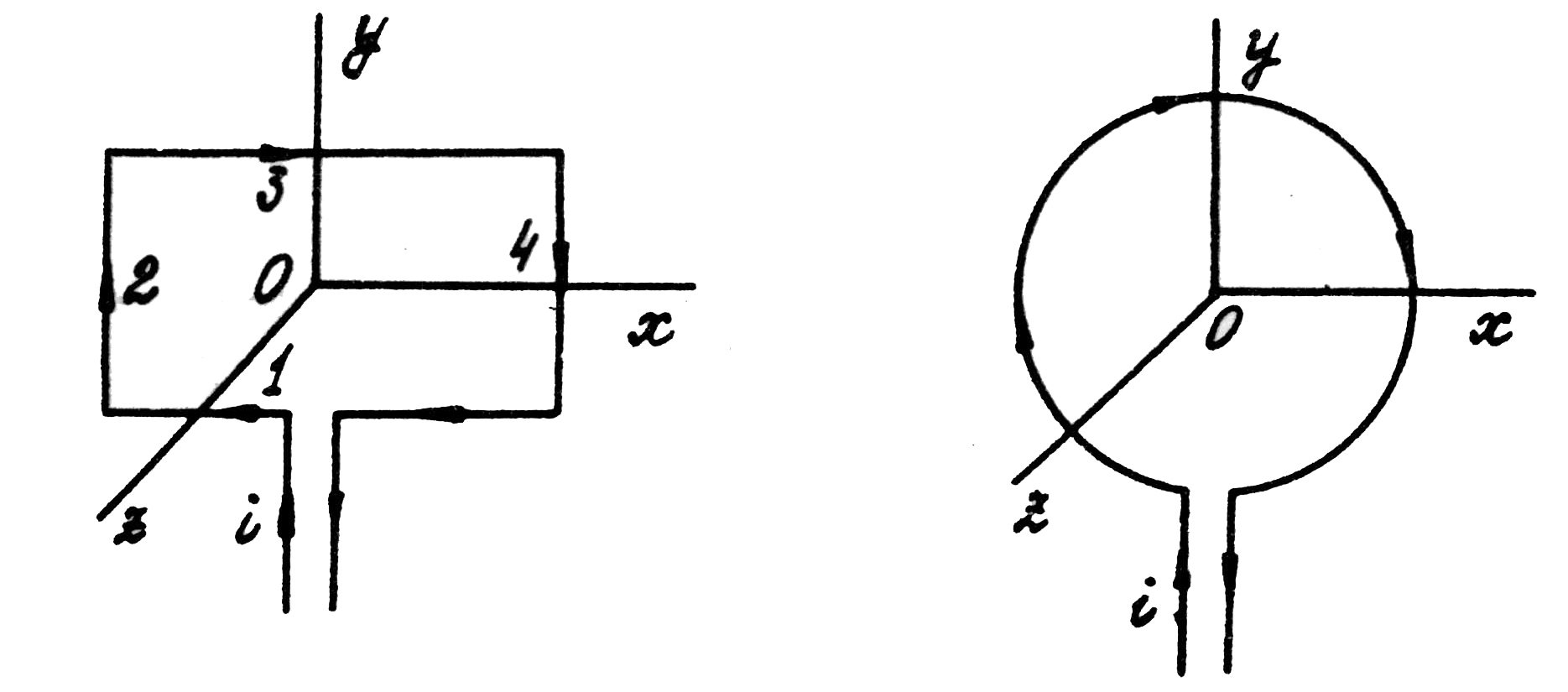
Рис. 6.8

С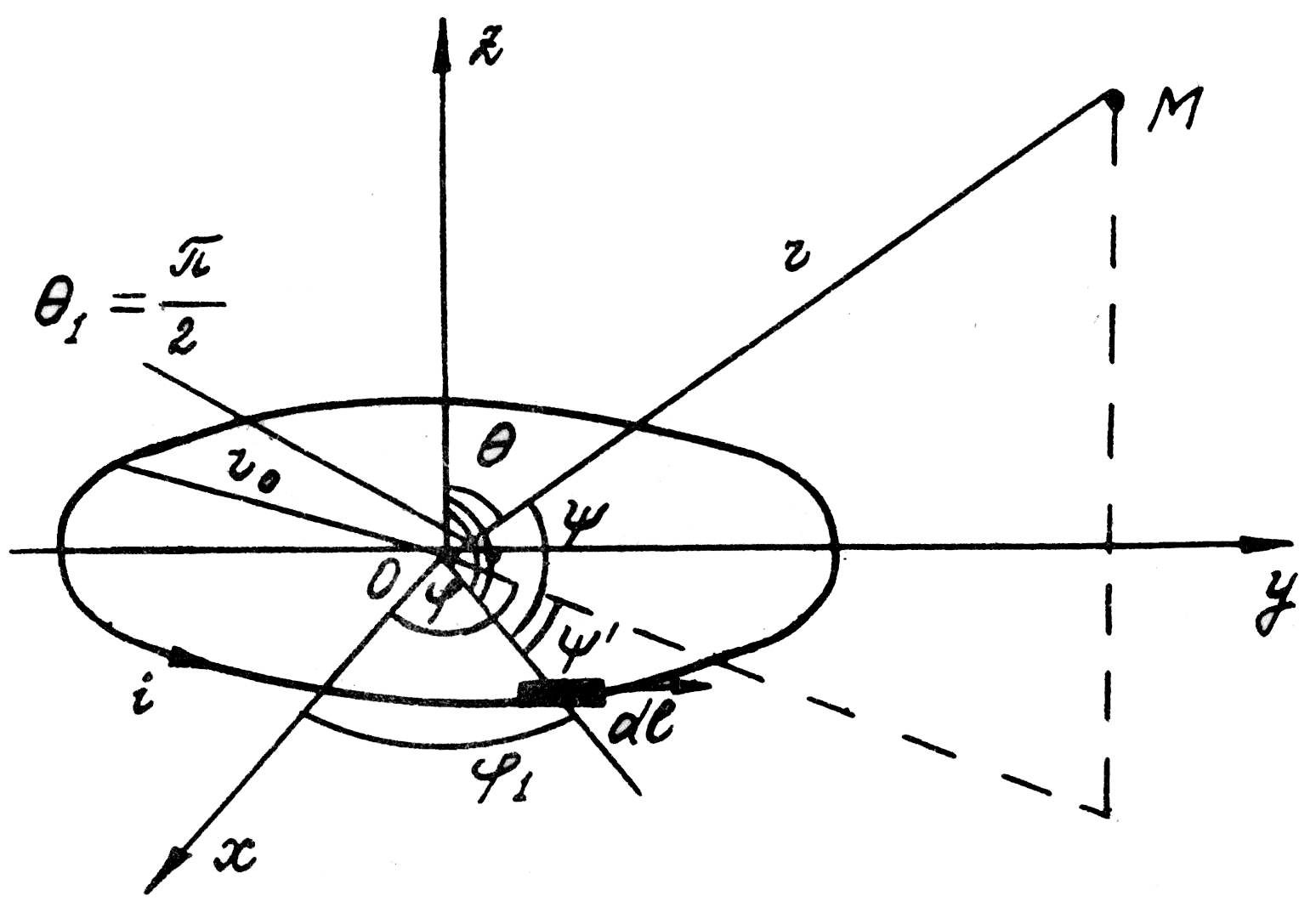 ледовательно, колебания поля, излучаемого каждой парой таких элементов, в точках на оси находятся в противофазе и компенсируют друг друга. Максимум излучения будет находиться в плоскости рамки, причём величина этого максимума будет обусловлена разностью хода волны; например, в направлении оси от плеча 2 до плеча 4 или от плеча 4 до плеча 2 в направлении оси разностью хода от плеча 1 до плеча 3 или от плеча 3 до плеча 1. Так как размеры рамки значительно меньше длины волны, то разность хода будет невелика, поэтому и излучение рамки с током невелико.

Рис. 6.9

Рассмотрим поле излучения рамочной антенны. Считаем, что амплитуда и фаза тока вдоль рамки постоянны, т. е. выполняется условие

Поле витка в точке наблюдения (рис. 6.9), расстояние до которой от витка велико по сравнению с радиусом витка , можно вычислить по общему правилу через электрический вектор-потенциал, определяемый формулой (6.2):

(6.28)

где

Применим эти формулы для рамки с током. Пусть рамка с током расположена в плоскости , тогда:

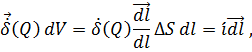
так как , где – площадь поперечного сечения провода рамки.

Обозначив , запишем:

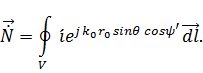
Вычислим вектор в сферической системе координат с ортами , , :

.

Вектор имеет три компоненты:

Так как рамка лежит в плоскости и симметрична относительно оси , то вектор имеет только одну составляющую , причём она не должна зависеть от угла . Поэтому достаточно вычислить , например, для :

Мы рассматриваем рамку, когда распределение тока вдоль неё постоянно, так как . При этом условии

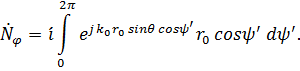
Так как , то

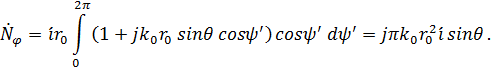
Следовательно, вектор-потенциал (6.28) запишется

Определим теперь составляющие электромагнитного поля рамки с током, используя выражения

Проделав вычисления по данным формулам для дальней зоны как , отбрасывая члены вида второй и выше степеней, получим:

(6.29)

Если сравнить эту формулу с формулой (6.16) для электрического диполя, то заметим, что характеристики направленности полей совпадают. Однако поля отличаются тем, что векторы электрического и магнитного полей поменялись местами.

Поляризация поля рамочной антенны отличается от поляризации поля электрического диполя. Электрический диполь имеет составляющие и , поляризация вертикальная. Магнитный диполь имеет составляющие и , поляризация горизонтальная.

Введём понятие действующей высоты рамки , тогда выражение (6.29) можно записать:

(6.30)

где , – площадь витка.

Получили, как и в случае электрического диполя, сферическую неоднородную волну. Поверхность постоянной фазы (сфера) , а поверхность постоянной амплитуды

Диаграмма направленности приведена на рис. 6.10.

а) – в меридиональной плоскости;

б) – в экваториальной плоскости.

Зависимость в ближней зоне аналогична, как и для электрического диполя.

Круговой контур с постоянным распределением тока вдоль него эквивалентен магнитному двойному слою с моментом . Очевидно, при переменном токе в витке момент также будет меняться и его комплексная амплитуда будет равна

Таким образом, формулу (6.29) можно переписать в виде:

и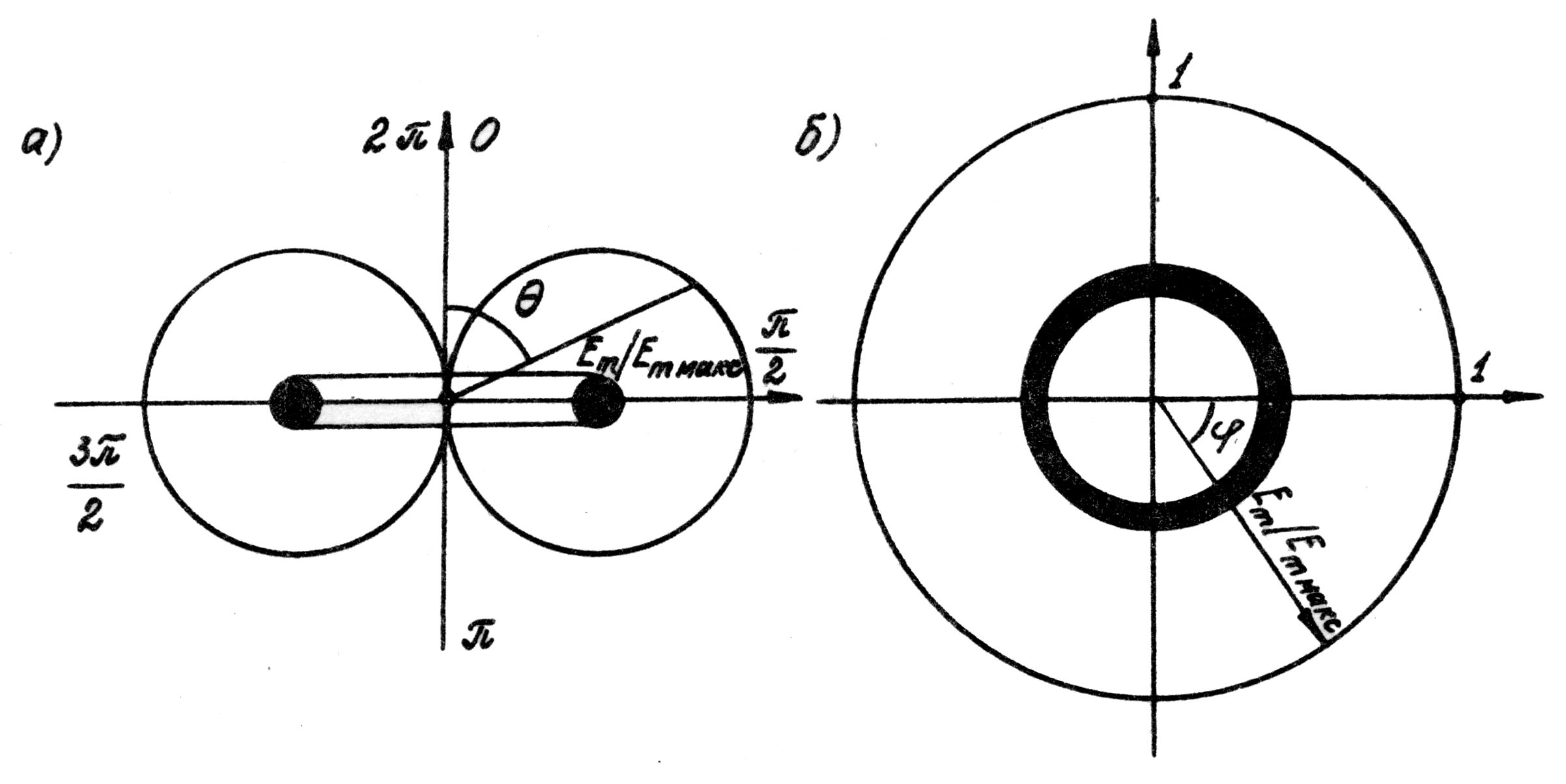 истолковать её как поле магнитного диполя с моментом , направленным по оси .

Рис. 6.10

Заметим, что использование представления о магнитном диполе применимо лишь при малой по сравнению с длиной волны рамкой, распределение тока в которой можно считать равномерным.

Если длина витка сравнима с длиной волны и, следовательно, распределение тока в нём неравномерное, то в этом случае поле следует вычислять, исходя из электрического вектор-потенциала.

Вычислим среднее значение вектора Умова – Пойнтинга для рамки с током (магнитного диполя):

(6.31)

Найдём мощность излучения :

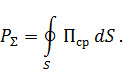
Простейшей замкнутой поверхностью является сфера, в центре которой расположена рамка. В этом случае

тогда

г

(6.32)

де – амплитуда тока в витке.

Определим сопротивление излучения магнитного диполя:

(6.33)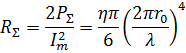

или

(6.34)

где – КНД магнитного диполя.( ).

Сравним основные параметры электрического и магнитного диполей. Для этого рассмотрим случай, когда . Здесь – длина витка рамочной антенны (магнитного диполя); – длина электрического диполя (т. е электрический диполь длины свёрнут в виток радиуса ).

Полагаем, что выполняется условие:

Сравним сопротивления излучения рамки и электрического диполя. Для электрического диполя по формуле (6.23)

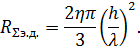
Сопротивление излучения витка равно:

.

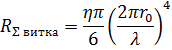Видим, что . Следовательно, с точки зрения излучения рамочная антенна хуже электрического диполя.

Сравним коэффициент полезного действия (КПД) рамки с током и электрического диполя одинаковых линейных размеров. КПД можно записать в виде:

(6.35)

При одинаковых линейных размерах витка и электрического диполя ( )

, но витка диполя.

Следовательно,

Отсюда видно, что КПД рамки с током меньше КПД электрического диполя.

Вследствие малого значения сопротивления излучения рамки с током и малого КПД, она редко используется в качестве излучателя электромагнитных волн. Рамка с током находит применение в качестве приёмной антенны, для которой КПД не имеет столь существенного значения, как для передающей. Применение рамочной антенны обусловлено направленностью её излучения.

Качество рамочной антенны улучшается за счёт увеличения действующей высоты , . Однако нужно помнить, что выражение для составляющих электромагнитного поля (6.30) справедливо при .

Действующую высоту рамки можно увеличить с помощью увеличения числа витков,т. е

где – число витков.

При этом также необходимо помнить, что должно выполняться условие .

Действующую высоту можно увеличить за счёт сердечника с соответствующей магнитной проницаемостью , на который наматывается рамка. В этом случае

где – магнитная проницаемость сердечника, она не совпадает с магнитной проницаемостью материала, из которого изготовлен сердечник за счёт размагничивающего влияния концов сердечника (обычно ):

где – относительная магнитная проницаемость сердечника;

– размагничивающий фактор.

Круговой виток с током (рамка с током) может рассматриваться как своеобразный тип излучателя, называемый магнитный.