4.7. Решение электродинамической задачи для идеального прямоугольного волновода

Рассмотрим прямоугольный идеальный волновод (рис. 4.10) , наиболее часто применяемый в технике СВЧ [6].

1. Будем рассматривать волну типа , т. е. за исходный возьмём магнитный вектор-потенциал Воспользуемся ранее полученными результатами:

(4.17)

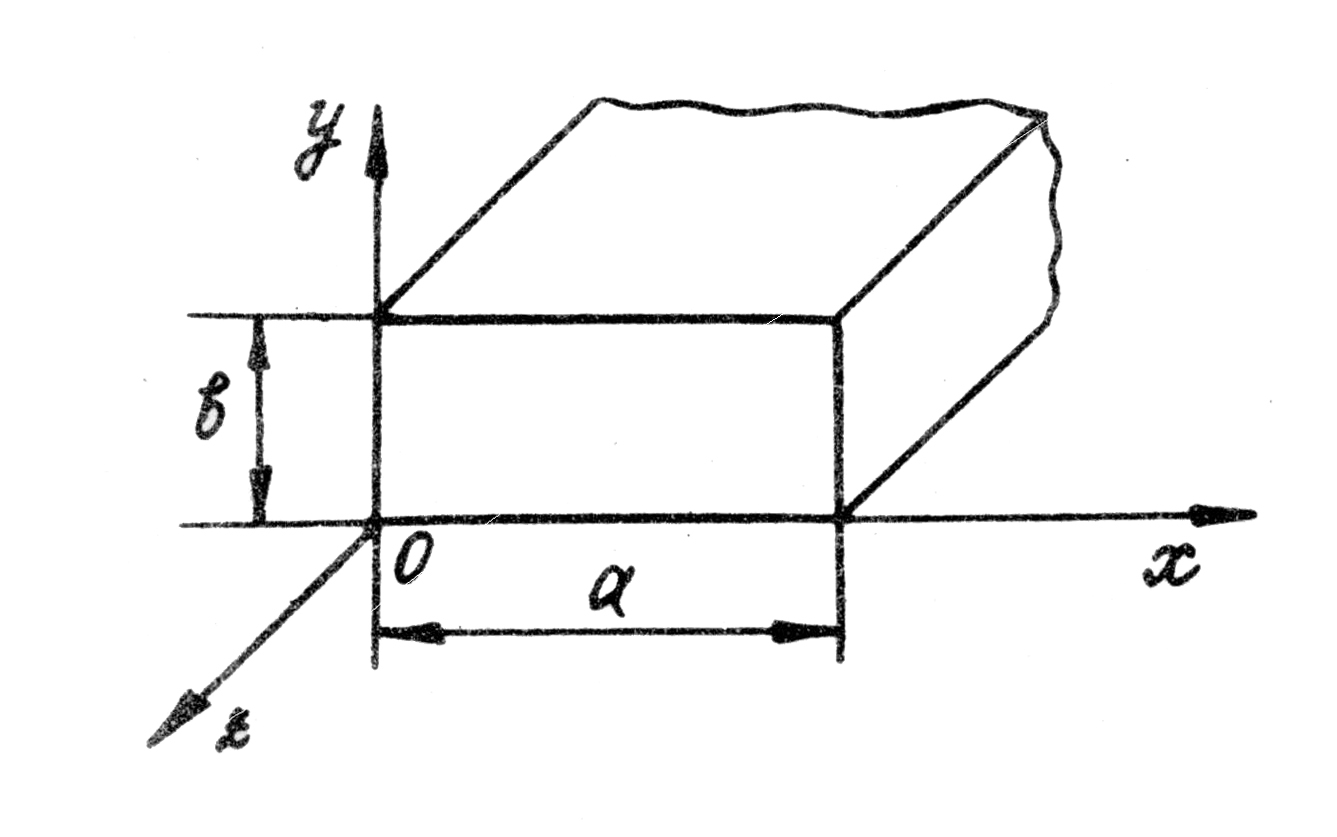
Рис. 4.10

Д

(4.18)

анное уравнение решается методом разделения переменных. Представим в виде произведения двух функций, из которых каждая зависит только от одной координаты:

Подставив (4.18) в (4.17) , получим:

(4.19)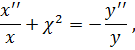

где – вещественное число, не зависящее от координат.

Правая часть уравнения (4.19) будет вещественным постоянным числом. Обозначим его , тогда имеем:

(4.20)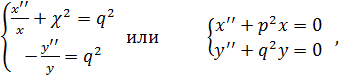

где , т. е. .

Решения данных уравнений будут иметь вид:

где , – произвольные постоянные;

– начальные фазы.

Вид выбранных решений объясняется тем, что мы ищем в поперечном сечении волновода стоячие волны. Следовательно,

(4.21)

В (4.21) неизвестны: Величина характеризует амплитуду и определяется условиями возбуждения. Определим

Для этого необходимы четыре уравнения. Запишем их, исходя из граничных условий, на соответствующих идеально проводящих стенках. Так как мы рассматриваем волну типа , то у данной волны могут быть только поперечные составляющие вектора . Поэтому используем условие, при котором тангенциальная составляющая вектора на идеально проводящей поверхности равна :

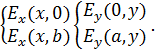
Продолжаем решать задачу

В дальнейшем для сокращения письма будем записывать

Подставляя , получим:

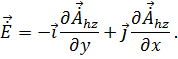
Поэтому то

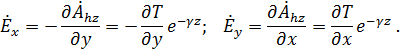
Найдём и . Подставляя выражение функции из (4.21), имеем:

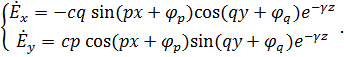
Применим к данным уравнениям граничные условия:

(4.22)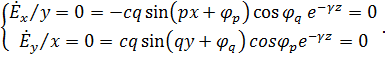

Условия (4.22) выполняются тогда, когда

Эти равенства будут выполняться, когда

(4.23)

Используем теперь два других граничных условия :

(4.24)

Условия (4.24) выполняются тогда, когда

или

(4.25)

Только при найденных значениях будут выполняться граничные условия, т. е. существовать электромагнитные волны в волноводе.

Запишем – функцию поперечного распределения:

(4.26)

Найдём – постоянную распределения. Но в соответствии с (4.20) . Следовательно,

(4.27)

где – постоянная распределения в волноводе.

Из (4.27) следует, что каждой паре чисел и волны типа будет соответствовать своя постоянная распространения. Волны, определяемые парами чисел и , называются парциальными волнами и обозначаются -волны. В волноводе может существовать бесконечное число парциальных волн, которые будут характеризоваться своими числами и .

Найдём составляющие электромагнитного поля в прямоугольном волноводе:

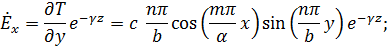
(4.28)

Составляющие напряжённости магнитного поля определяются из выражения

Раскрывая это выражение, получим

(4.29)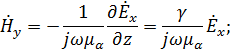

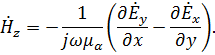
Обозначим

(4.30)

где – характеристическое сопротивление для - волны.

Тогда

(4.31)

Найдём . Так как

следовательно,

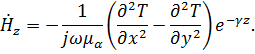
Но функция удовлетворяет условию (4.17), поэтому

(4.32)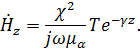

Формулы (4.28 – 4.29), (4.31 – 4.32) определяют электромагнитное поле в прямоугольном волноводе для - волны.

2. Аналогично можно получить выражения для составляющих электромагнитного поля типа . В качестве исходного необходимо взять электрический вектор-потенциал :

Для определения постоянных для данного типа волны используются следующие граничные условия: у данной волны, как известно, имеется составляющая вдоль оси волновода, поэтому необходимо потребовать, чтобы эта составляющая на всех стенках была равна нулю:

Сделав аналогичный вывод, получим:

Составляющие электромагнитного поля при этом запишутся:

(4.33)

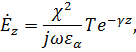
где – характеристическое сопротивление для -волны . Формулы (4.33) определяют электромагнитное поле для -волны.

Из полученных результатов можно сделать следующие основные выводы:

1. Индексы и указывают на число стоячих полуволн, укладывающихся вдоль размеров и соответственно. Решение для составляющих электромагнитного поля, соответствующее определённым целым значениям пары чисел и , называются парциальными волнами и обозначаются - или -волнами.

2. В прямоугольном волноводе не может распространяться волна типа , так как поперечные составляющие , обращаются в ноль ).

3. В прямоугольном волноводе не могут существовать волны типа и , так как в этом случае вектор-потенциал равен нулю и составляющие поля пропадают.

4. Любой парциальной волне соответствует вполне определённая постоянная распространения:

где – волновое число волновода для данного типа волны.

Для того чтобы волна распространялась, необходимо, чтобы было действительным числом:

При этом должно выполняться условие:

Величина нызывается критической длиной волны в волноводе:

З

(4.34)

амечаем, что если , то распространение волны в волноводе возможно. Если , то соответствующая волна не будет распространяться в волноводе, так как будет чисто вещественным числом, а это соответствует тому, что волна будет затухать по экспоненциальному закону от места её возникновения.

Волны, для которых , называются местными. При строгом решении задачи данные волны необходимо учитывать, особенно в местах неоднородностей и в месте возбуждения колебаний. Можем записать:

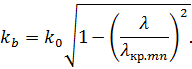
Найдём длину волны в волноводе, т. е. ,

(4.35)

Из (4.35) следует, что длина волны в волноводе не равна длине волны в свободном пространстве:

5. Характеристическое сопротивление для -волны

(4.36)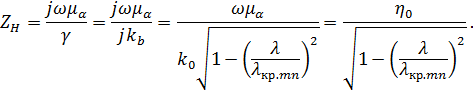

где – волновое сопротивление среды, заполняющей внутреннюю полость волновода.

Видим, что .

Характеристическое сопротивление для -волны

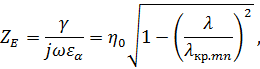
т. е. . Замечаем, что

Характеристические сопротивления в литературе называют волновым сопротивлением по полю.

Таким образом, в прямоугольном волноводе могут распространяться волны:

Данные волны могут существовать и распространяться в волноводе, причём совместно, если выполняется условие для этих волн.

На практике стремятся, чтобы электромагнитная энергия передавалась на одной волне. Для этого необходимо, чтобы для данной волны выполнялось условие , а для остальных волн должно выполняться условие . В таблице приведены значения , рассчитанные в соответствии с формулой (4.34) .

Тип волны
	2a	2b		a	b

Из приведённой таблицы следует, что для существования в волноводе одной волны, например , должны быть выполнены условия:

Если же , что практически выполняется, то условие существования волны будет одно;

при -волна имеет наибольшую критическую длину волны, поэтому она называется основной волной прямоугольного волновода.

Кроме этой особенности, волна обладает рядом других преимуществ по сравнению с другими типами волн:

имеет наиболее простую структуру поля и наиболее легко возбуждается в волноводе;

с помощью волны при данном поперечном сечении волновода можно передать максимальную мощность;

затухание мощности на единицу длины волновода меньше, чем для других волн.

В силу этих особенностей волна нашла наиболее широкое распространение в технике СВЧ.

Запишем составляющие воля волны . Для этого в выражениях (4.28 – 4.29) и (4.31 – 4.32) для

-волны положим . Получим:

(4.37)

(4.38)

Из (4.38) следует, что волна имеет только три компоненты .

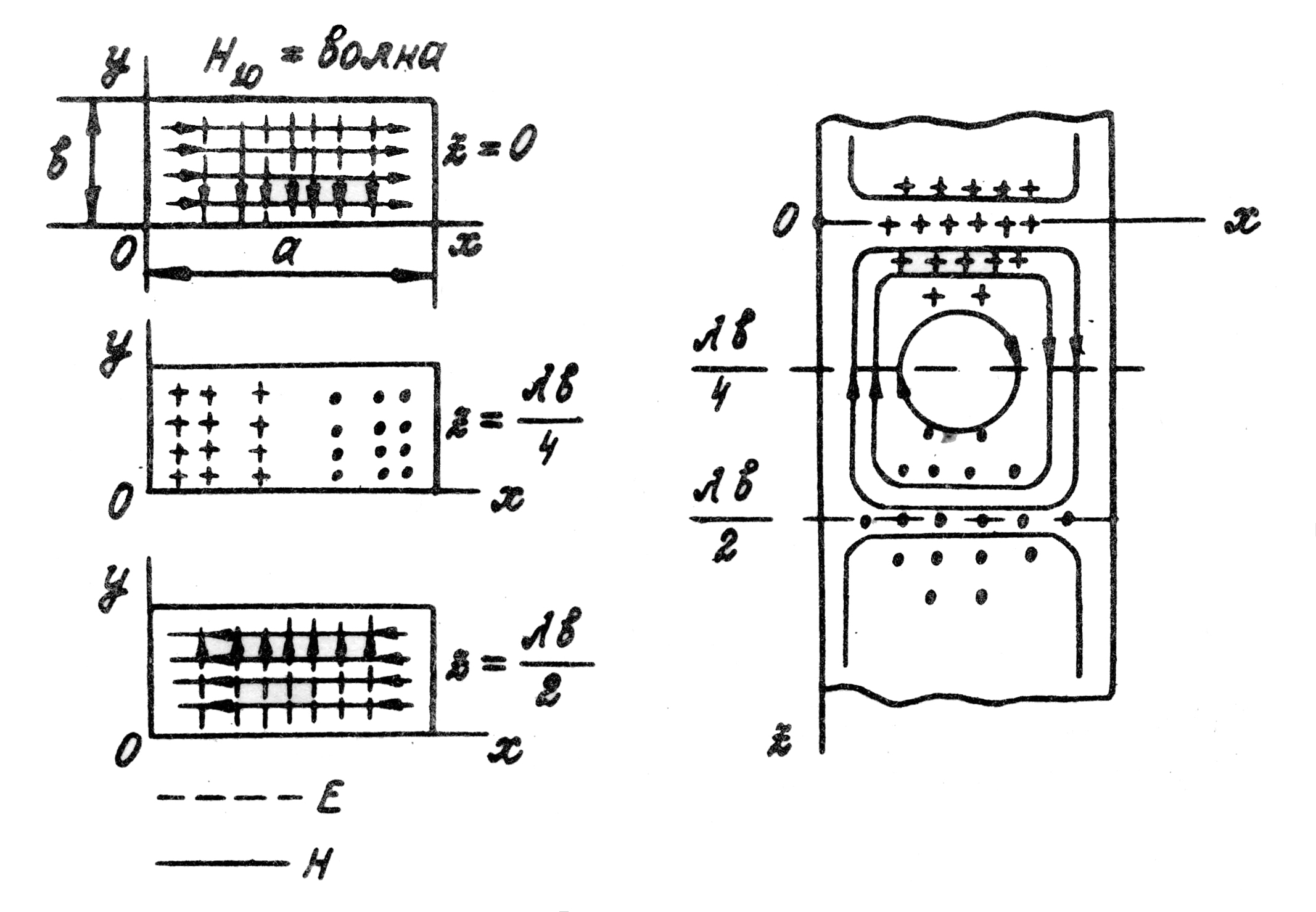
Рис. 4.11

Для мгновенных значений составляющих вектора поля получим:

(4.39)

Формулы (4.39) показывают, что и изменяются в противофазе друг с другом, а составляющая сдвинута по фазе относительно и на четверть периода, причём в сторону отставания по отношению к . На рис. 4.11 приведены картины силовых линий поля волны в различных сечениях волновода при