1.2. Закон сохранения электрического заряда

Согласно лежащему в основе теории электричества закону сохранения электрического заряда, электрические заряды не могут ни возникать, ни исчезать, они лишь могут перемещаться в пространстве.

Если рассматривается какая-либо замкнутая система, то количества отрицательных и положительных зарядов сохраняются постоянными и изменение электрического состояния системы сводится лишь к перераспределению этих зарядов в пространстве.

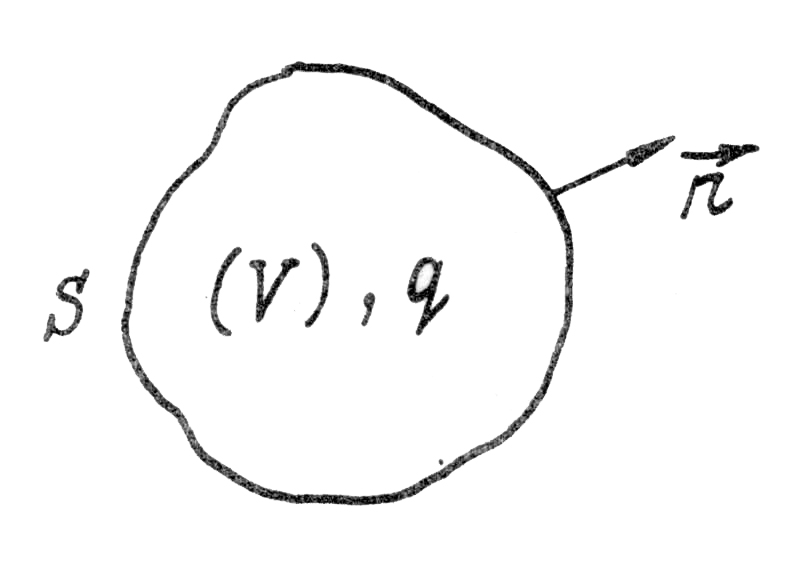
Рис. 1.3

Если из какого-либо объёма вытекает электрический ток (рис. 1.3), внутри заряд уменьшается, т. е.

(1.8)

Формула (1.8) представляет собой интегральное выражение закона сохранения электрического заряда.

От интегральной формы перейдём к дифференциальной. Если внутри объёма заряд распределён с объёмной плотностью , то Учитывая это из (1.8) имеем

Следовательно,

(1.9)

Выражение (1.9) справедливо при сколь угодно малом объёме . Для конечного объёма можно записать

Эта формула будет точной, если . Возьмём предел отношения

Этот предел может быть вычислен и в математике, он называется дивергенцией (расхождением) вектора и обозначается , т. е.

Из курса математики известно, что вектора в прямоугольной системе координат вычисляется следующим образом:

Таким образом, получим:

(1.10)

Выражение (1.10) представляет дифференциальную форму закона сохранения электрического заряда. Эту формулу также называют уравнением непрерывности ( и должны удовлетворять условиям конечности и непрерывности в любой точке рассматриваемой области).

В (1.9) заменим по формуле (1.10), получим

Э

(1.11)

то выражение есть формула Остроградского. Она является общей формулой преобразования поверхностного интеграла в объёмный и справедлива для любого вектора, который непрерывен вместе со своими производными во всех точках объёма и на ограничивающей его поверхности .

Если в каждой точке определённой области плотность заряда постоянна во времени, т. е. , то ток, входящий в эту область через ограничивающую замкнутую поверхность , должен быть всё время равен току, выходящему наружу. В этом случае из (1.9) имеем:

а из (1.10) следует, что . Если функции, описывающие процесс, не зависят от времени, то такой процесс, как известно, называется стационарным.

Таким образом, стационарное течение электричества определяется вектором , который в каждой точке области постоянен по величине и направлению. Так как распределения стационарного тока всюду равна нулю, то в стационарном состоянии все линии тока замкнуты сами на себя. Иными словами, поле вектора при постоянном токе является соленоидальным.

Рассмотренный здесь ток представляет движение электрических зарядов. Поскольку среды, в которых наблюдается движение электрических зарядов, называются проводящими, то рассмотренный нами ток называется током проводимости.

1.3. Вектор напряжённости электрического поля и вектор электрической индукции

Между электрическими зарядами имеется взаимодействие. Впервые это взаимодействие было обнаружено Кулоном. Если имеем 2 точечных заряда и , то сила взаимодействия между зарядами определяется выражением

(1.12)

Выражение (1.12) есть закон Кулона, где – коэффициент, зависящий от свойств среды и выбора систем единиц. Данное взаимодействием обусловлено взаимодействие электрических полей данных зарядов.

Поле заряда определяется его напряжённостью , которая равна той силе, которую испытывает единичный точечный заряд, помещённый в данную точку поля:

(1.13)

,

г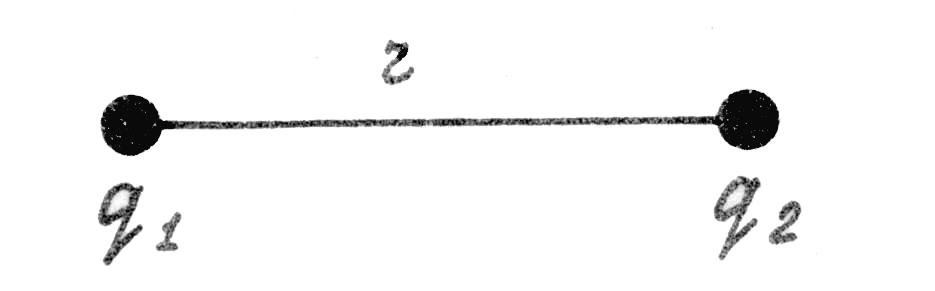 де – единичный вектор, который вводится для определения направления вектора .

Рис. 1.4

Значение зависит от свойств среды (коэффициент ). Это затруднение можно устранить путём введения дополнительного вектора – вектора электрической индукции или вектора смещения – . Этот вектор был введён Максвеллом путём высказанного им постулата: поток вектора через любую замкнутую поверхность (см. рис. 1.3) при любом распределении заряда внутри этой поверхности и независимо от свойств среды равен количеству электричества (заряду), находящемуся внутри этой поверхности:

(1.14)

Выражение (1.14) представляет постулат Максвелла.

Если заряд распределён внутри объёма с объёмной плотностью , то Поэтому (1.14) можно записать в виде

(1.15)

Формула (1.15) есть интегральная форма постулата Максвелла.

Если под интегральные функции в объёме и на ограничивающей его поверхности непрерывны, то, применив к (1.15) формулу Остроградского, (1.11) получим:

Следовательно,

(1.16)

.

Это дифференциальная форма постулата Максвелла. Она показывает, что заряды, распределённые с объёмной плотностью являются источником вектора . Отсюда видим, что не зависит от свойств среды.

Поле вектора удобно представить в виде линий вектора , в каждой точке которых вектор совпадает по направлению с касательной к этой линии (рис. 1.5), непосредственно в месте расположения заряда. Вне заряда так

Рис. 1.5

Таким образом, при наличии электрических зарядов, линии вектора должны быть разомкнуты, начинаясь на положительном заряде и кончаясь на отрицательном.