4.4. Групповая скорость

Понятие групповой скорости вводится при распределении пучка монохроматических волн, частоты которых мало отличаются от некоторой средней частоты. Для пояснения этого понятия рассмотрим простейший случай двух синусоидальных волн одинаковой и неизменной амплитуды, распространяющихся вдоль оси . Положим, амплитуды колебаний равны единице. Частота 1-й волны и волновое число . Частота 2-й волны и волновое число . Суммарная волна будет иметь вид:

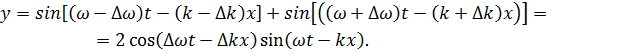
Это выражение показывает, что результирующее колебание представляет собой высокочастотную волну с частотой и фазовой скоростью , амплитуда которой медленно меняется во времени с частотой Амплитуда этой волны перемещается со скоростью .

Скорость перемещения амплитуды (но не фазы) результирующего колебания и называется групповой скоростью волнового процесса. Следовательно, групповая скорость:

Понятие групповой скорости применимо лишь к таким колебаниям, которые ограничены узкой полосой спектра. Скорость перемещения средней амплитуды волнового пакета как раз и равна групповой скорости:

Если то для монохроматической волны скорость распространения волны равна скорости света. Аналогично можно найти скорость распространения волны между зеркалами:

4.5. Некоторые типы волн между зеркалами

Рассмотрим составляющие некоторых волн между зеркалами.

1) Для - волн:

(4.7)

Приведённые выражения показывают, что волны с индексом не существует. Так, например, для волны Огибающие составляющие поля этой волны приведены на рис.4.7.

2) Для - волн:

(4.8)

Заметим, что волна нулевого порядка с может существовать между зеркалами. При этом замечаем, что , т. е. эта волна отличается от парциальных и -волн ( ) тем, что она полностью поперечная и может быть возбуждена источником любой частоты. Эта волна имеет наибольшую критическую длину волны и называется основной волной. Таким образом, при волна типа вырождается в волну типа .

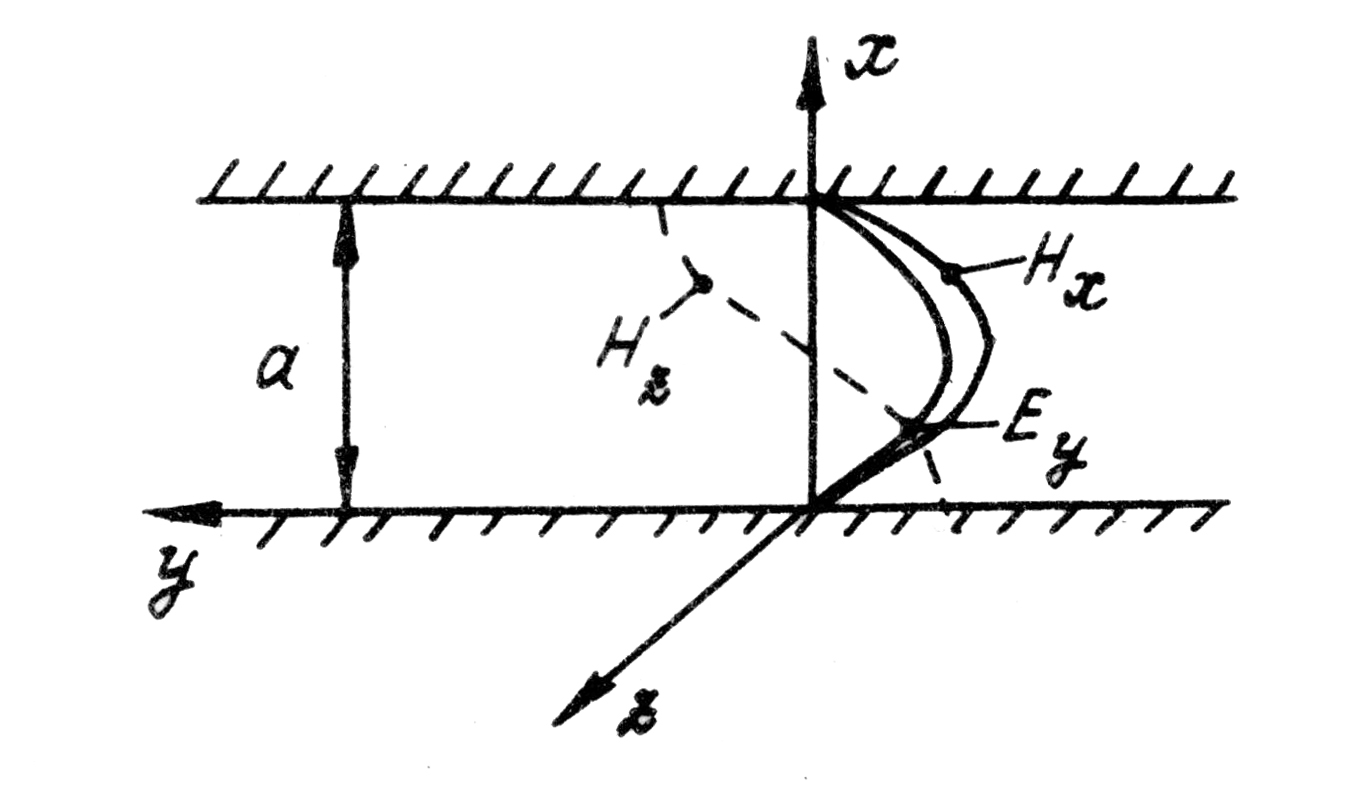
Рис. 4.7

При работе системы из двух зеркал часто требуется, чтобы в этой системе существовал одномодовый режим, т. е. могла распространяться только одна волна. Такой режим встречается при передаче электромагнитной энергии. Поэтому выбирают основную волну, имеющую наибольшую критическую длину волны. В этом случае . Следовательно, , т. е. волна падает касательно идеально проводящей плоскости. Для того чтобы данная волна могла распространяться в такой системе, необходимо взять Чтобы не возникли другие волны с индексами , необходимо выполнить условие (для ). Так, при для волн типа и . Следовательно, условие одномодового режима при работе основной волны следующие:

(4.9)

П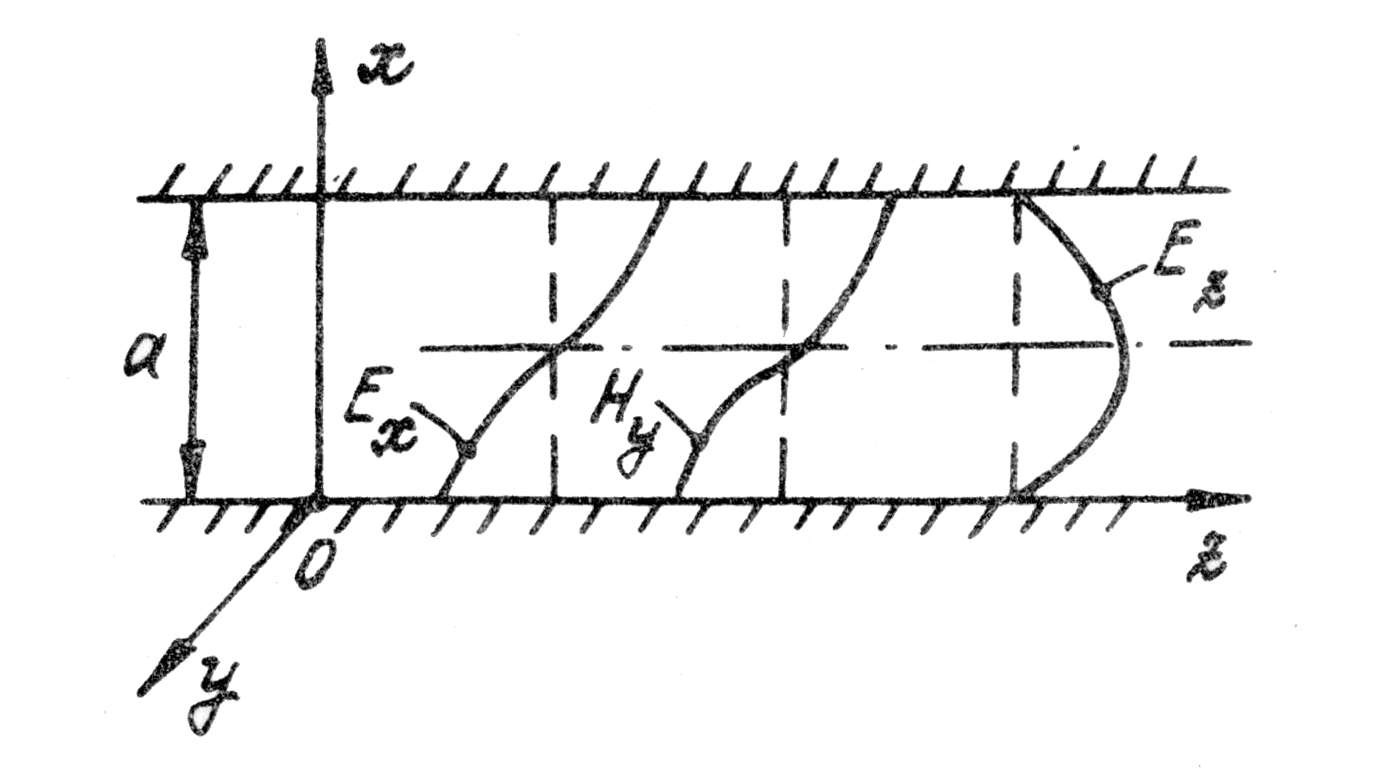 ри этом для волн более высших порядков это условие будет выполняться и подавно.

Рис. 4.8

Для других парциальных волн эти волны будут типа . Так при получаем -волну, у которой Огибающие составляющих поля этой волны приведены на рис. 4.8.

4.6. Общее решение задачи для идеального волновода

В дальнейшем будем рассматривать цилиндрические волноводы. Под цилиндрическими поверхностями понимаются, как известно, поверхности, образованные перемещением прямой линии по замкнутому контуру параллельно этой прямой.

По форме поперечного сечения волноводы бывают: прямоугольные, круглые и др. Наиболее широко в настоящие время применяются в радиотехнике прямоугольные волноводы.

На основании полученных результатов процесса распространения электромагнитных волн между двумя зеркалами естественно предположить, что для волновода этот процесс может быть так же интерпретирован, как результат наложения отражённых стенками волновода элементарных волн. Однако использование применённого для случая двух зеркал наглядного метода исследования в волноводе встречает трудности из-за сложности геометрических построений.

Поэтому решение задачи в волноводе основывается на применении или непосредственного решения уравнений Максвелла внутри волновода, или используются вспомогательные векторы: вектор-потенциал или вектор Герца.

Воспользуемся вектор-потенциалом. Будем рассматривать условия распространения электромагнитных колебаний в волноводе, считая, что: сторонние токи и заряды равны нулю; стенки волновода идеально проводящие; среда внутри волновода – идеальный диэлектрик.

В такой области вектор-потенциал как электрический, так и магнитный для периодически меняющихся процессов удовлетворяет уравнению

(4.10)

где – волновое число для случая идеального диэлектрика, заполняющего внутреннюю полость волновода.

У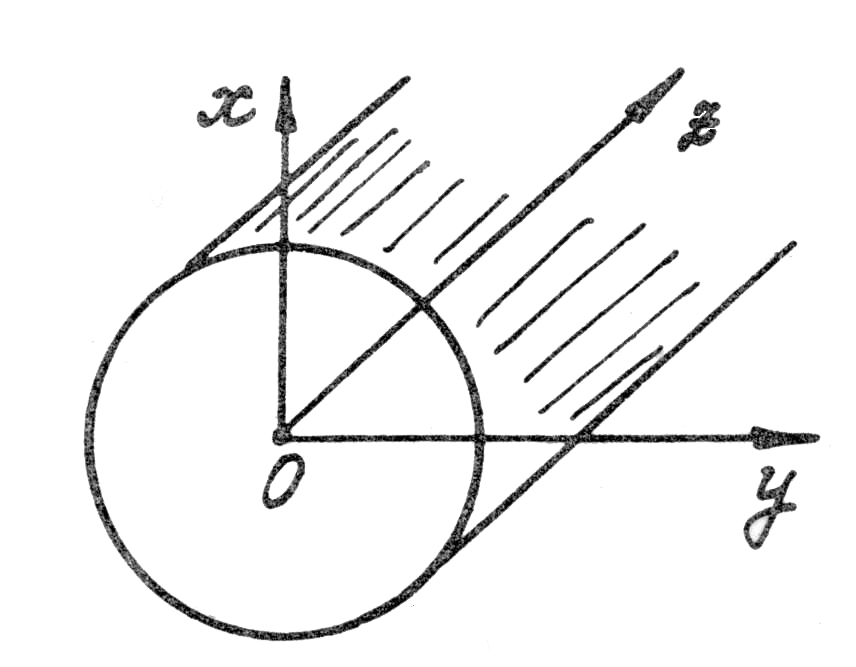 равнение (4.10) имеет бесконечное множество решений и решать задачу можно двояко: можно брать частное решение и, используя граничные условия на стенках волновода, найти решение, которое нас удовлетворяет; сделать некоторые предвидения для ожидаемого решения для вектор-потенциала.

Рис. 4.9

Так как мы интересуемся электромагнитным процессом, распространяющимся вдоль оси (рис. 4.9), то распределение поля в поперечном сечении будет отличаться от распределения вдоль оси . В поперечном сечении будут стоячие волны. Вдоль оси характер поля зависит от нагрузки. Если волновод бесконечный, то будем наблюдать бегущую волну. Если же имеется нагрузка и она не согласована, то будет ещё и отражённая волна. Так как стенки идеально проводящие, то волна должна быть плоской и, следовательно, поверхность постоянной фазы будет плоскость. Поскольку волновод цилиндрический, то сечение вдоль оси одинаково и не зависит от .

Исходя из этого, вектор-потенциал будем искать в виде:

(4.11)

где – единичный вектор;

– вещественная функция поперечного распределения поля;

– постоянная распространения, в общем случае комплексное число.

Так как стенки волновода идеально проводящие и диэлектрик идеальный, то – чисто мнимое число.

Вспомним, что для неограниченной среды вектор-потенциал выбирался в виде , так как никаких ограничений по направлениям не было. Необходимо отыскать такую функцию , которая удовлетворяла бы граничным условиям на стенках волновода. Подставив (4.11) в (4.10) , получим:

или

(4.12)

где (4.13)

При выполнении граничных условий мы получим вполне определённые , которым будут соответствовать вполне определённые . Для того, чтобы волна распространилась, т. е. было чисто мнимым, необходимо выполнить условие:

(4.14)

Если условие (4.14) не выполняется, то волна затухает. Далее, если мы решим уравнение (4.11), затем выразим через вектор-потенциал вектора и , то мы решим поставленную задачу. Для облегчения решения задачи обычно принимают направление вектор-потенциала вдоль оси , т. е. . Следовательно,

где

Если за исходное возьмём электрический вектор-потенциал , т. е.

тогда векторы поля и определятся по формулам:

(4.15)

уравнение связи.

Вычисления по (4.15) показывают, что

Таким образом, если за исходное берём электрический вектор-потенциал , то получаем решение, соответствующее волне типа , т. е. волне, у которой магнитное поле имеет только поперечные составляющие.

Если за исходное возьмём магнитный вектор-потенциал ,т. е.

,

тогда векторы поля и определятся по формулам:

(4.16)

уравнение связи.

Вычисления по (4.16) показывают, что

Таким образом, если за исходное берём магнитный вектор-потенциал то получаем решение, соответствующее волне типа , т. е. волне, у которой электрическое поле имеет только поперечные составляющие.

В результате, проделав вычисления по формулам (4.15) или (4.16), мы решим поставленную задачу в общем виде. Опуская эти достаточно громоздкие вычисления, которые читатель при необходимости может проделать самостоятельно по приведённой схеме, приведём лишь основные физические выводы:

в любом поперечном сечении волновода, т. е. при , силовые линии электрического и магнитного полей ортогональны;

условие в сечении соответствует уравнению силовых линий в поперечном сечении волновода для вектора у -волны и для вектора у -волны;

для -волны составляющая пропорциональна электрическому вектор-потенциалу (или функции ). Остальные составляющие поля могут быть выражены через составляющую

для -волны составляющая пропорциональна магнитному вектор-потенциалу потенциалу (или функции ). Остальные составляющие поля могут быть выражены через составляющую

о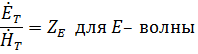 тношение поперечных составляющих электрического и магнитного полей для прямой и обратной волн порознь равно характеристическому сопротивлению:

-волны

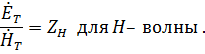
-волны

где