4.3. Общие условия распространения электромагнитных волн между двумя плоскими параллельными зеркалами
Два
параллельных зеркала представляют
собой своеобразный волновод, ширина
которого безгранична (рис. 4.6). Выше было
установлено, что над плоскостью зеркала
образуется поле, в котором на плоскостях
непроницаемости, параллельных зеркалу
и находящихся от него на расстояниях
составляющие
поля принимают такие же значения, как
и на самом зеркале. На этих плоскостях
выполняются граничные условия,
соответствующие идеально проводящей
поверхности.
Таким образом, если любую из воображаемых плоскостей непроницаемости заменим идеальным зеркалом, то поле между зеркалами останется таким же, как и прежде, так как оно удовлетворяет граничным условиям Максвелла.
П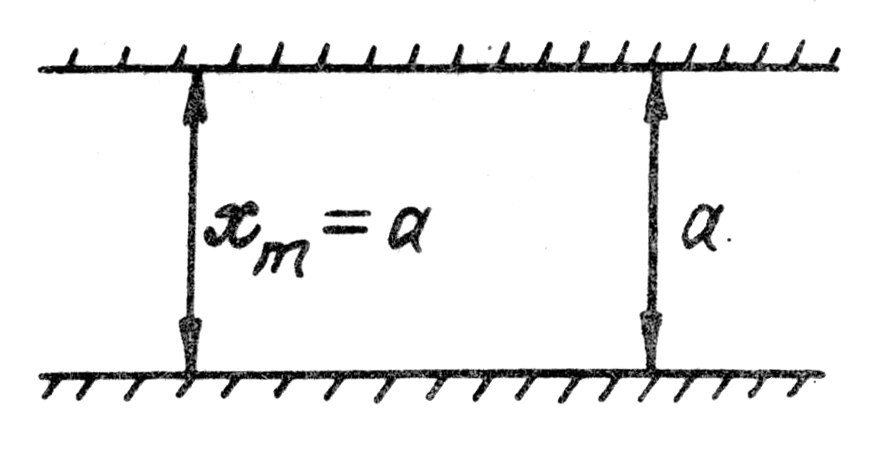
рактически
же зеркала отстоят друг от друга на
определённом расстоянии 
и требуется определить поле между
зеркалами. Это поле будет таким же, как
и прежде, если взять:
Рис. 4.6
Отсюда
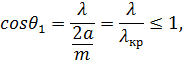
здесь
обозначено 
,
– критическая длина волна.
Следовательно, необходимо, чтобы выполнялось условие
Полученные ранее формулы показывают, что любая из составляющих поля распространяется по закону
где
где – постоянная распространения.
Замечаем,
что при 
будет чисто мнимой величиной, а 
будет иметь смысл волнового числа.
Причём в этом случае вдоль оси
будет
распространяться незатухающая
электромагнитная волна.
Решение
будет существовать и тогда, когда 
.
Физически такое решение будет
соответствовать полю, которое не является
волновым. Оно быстро затухает по
экспоненциальному закону с увеличением
.
Анализ указанных положений позволяет сделать следующие выводы.
1) Незатухающие электромагнитные волны между двумя зеркалами существуют только в том случае, если
где
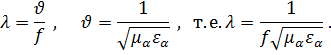
Но
соответствует
критическая частота 
.
Поэтому для существования волны
необходимо
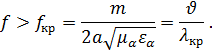
2) Волновое число, характеризующее распространяющуюся волну между зеркалами,
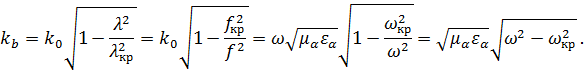
Длина волны тогда выразится:
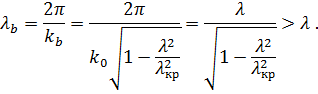
Фазовая скорость волны между зеркалами будет:
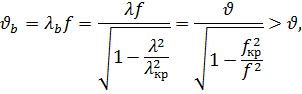
т. е. фазовая скорость между зеркалами больше скорости света между ними и зависит от частоты.
3)
Величины , кроме зависимости от
,
зависят и от целого числа
.
Таким образом, не всякие волны образуются
между зеркалами, а только такие, когда
– целое число. Волны, соответствующие
целому числу
,
называются парциальными волнами порядка
Например, 
– электрическая волна порядка
;
– магнитная волна порядка
.
Таким образом, между зеркалами может существовать безграничное число парциальных волн как электрических, так и магнитных.
Возникновение того или иного типа волны зависит от источника, создающего эти волны, и определяется значение критической длины волны:
Если
,
то
,
т. е. необходимо 
.
Если
,
то 
,
т. е. необходимо 
.
Но в этом случае и подавно
,
следовательно, возникает 2-я парциальная
волна.
4) Для определения мощности, передаваемой волны, определим среднее значение вектора Умова – Пойнтинга:
Для
-
волн:
следовательно,
Вычислив, получим:
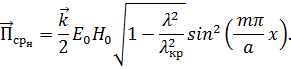
Для
-
волн:
следовательно,
Вычислив, получим:
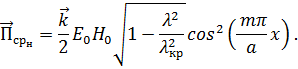
При вычислениях учтено, что
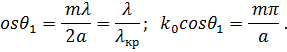
Зная выражение для вектора Умова – Пойнтинга, можно вычислить скорость движения энергии, исходя из физических соображений:
следовательно,
(4.6)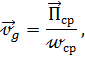
где
скорость
движения энергии;
средняя
объёмная плотность электромагнитной
энергии.
Вычисления по формуле (4.6) приводят к следующему результату:
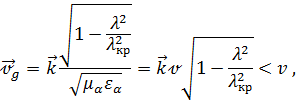
где
скорость света в данной среде.
Скорость
движения энергии меньше скорости света.
Заметим, что 
Покажем, что скорость 
совпадает
с групповой скоростью. Понятием этой
скорости широко пользуются в квантовой
механике.